
Çeşitkenar Üçgen Nelerdir?
Çeşitkenar üçgen, kenar uzunlukları eşit olan bir üçgendir. Bu özelliği sayesinde simetrik bir yapıya sahiptir ve iç açılarının her biri 60 derece olarak belirlenir. Geometri ve matematikte önemli bir yere sahip olan çeşitkenar üçgenler, pratik uygulamalarda da sıkça kullanılır.
Çeşitkenar Üçgen Nedir?Çeşitkenar üçgen, tüm kenar uzunlukları eşit olan bir üçgendir. Bu eşitlik, üçgenin simetrik bir yapıya sahip olmasını sağlar ve üçgenin iç açılarının da eşit olmasına yol açar. Çeşitkenar üçgenlerde, her bir iç açı 60 derece olarak ölçülür. Bu özellikleri sayesinde, çeşitkenar üçgenler geometri ve matematikte önemli bir yere sahiptir. Çeşitkenar Üçgenin Özellikleri Çeşitkenar üçgenlerin belirgin özellikleri vardır:
Çeşitkenar Üçgenin Çizimi Çeşitkenar bir üçgen çizmek oldukça basittir. Aşağıdaki adımları izleyerek bir çeşitkenar üçgen çizebilirsiniz:
Çeşitkenar Üçgenin Kullanım Alanları Çeşitkenar üçgenler, mimarlık, mühendislik ve sanat gibi birçok alanda kullanılmaktadır. Özellikle, yapıların dayanıklılığı ve estetiği açısından önemlidir. Çeşitkenar üçgenler, aynı zamanda matematiksel problemlerde de sıklıkla karşılaşılır.
Sonuç Çeşitkenar üçgenler, sahip oldukları eşit uzunluktaki kenarları ve açılar nedeniyle geometri ve matematikte önemli bir yere sahiptir. Bu üçgen türü, hem teorik hem de pratik alanlarda geniş bir kullanım yelpazesine sahiptir. Çeşitkenar üçgenlerin özellikleri, çizimi ve kullanım alanları, öğrencilerin geometri anlayışını geliştirmek için temel bir konu olarak öne çıkmaktadır. |
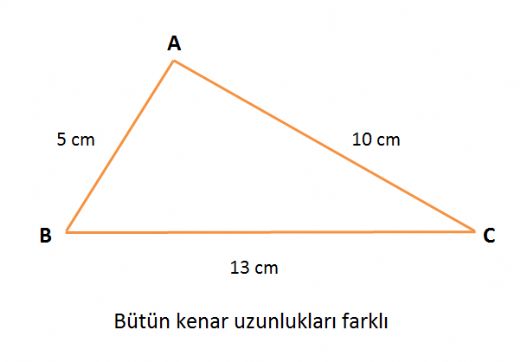





























Çeşitkenar üçgen çevre hesaplama nasıl yapılır
Çeşitkenar Üçgen Nedir?
Çeşitkenar üçgen, üç kenarı ve üç açısı da eşit olan bir geometrik şekildir. Her bir kenarının uzunluğu birbirine eşittir ve her bir açısı 60 derecedir.
Çeşitkenar Üçgenin Çevresi Nasıl Hesaplanır?
Çeşitkenar üçgenin çevresini hesaplamak oldukça basittir. Çevre, üç kenarın toplam uzunluğudur. Eğer a, b ve c kenar uzunlukları ise, çevre (C) şu şekilde hesaplanır:
C = a + b + c
Çeşitkenar üçgen olduğu için, a = b = c olur. Dolayısıyla, kenar uzunluğunu (a) bildiğimizde, çevre formülü:
C = 3a şeklinde olur.
Örnek Hesaplama
Eğer bir çeşitkenar üçgenin kenar uzunluğu 5 cm ise, çevresi:
C = 3 5 = 15 cm olacaktır.
Bu şekilde çeşitkenar üçgenin çevresini kolayca hesaplayabilirsiniz.
Çeşitkenar üçgenin çevresi nasıl bulunur sorusu, geometri derslerinde sıkça karşımıza çıkan bir konudur. Üçgenin tüm kenar uzunluklarını toplamak yeterlidir. Örneğin, kenar uzunlukları a, b ve c ise çevre P = a + b + c formülüyle hesaplanır. Bu şekilde, üçgenin çevresini kolayca bulabilirsiniz.
Merhaba Aksungur,
Çeşitkenar üçgenin çevresinin nasıl bulunacağı konusunu oldukça iyi özetlemişsiniz. Kenar uzunluklarını toplamak, bu tür geometrik şekillerin çevresini bulmanın en temel yöntemidir. Özellikle a, b ve c gibi kenar uzunluklarını kullanarak P = a + b + c formülü ile çevreyi hesaplamak, matematik derslerinde sıkça karşılaşılan bir uygulamadır.
Bu bilgiyi pekiştirerek, öğrencilere üçgenin çevresini bulurken dikkat etmeleri gereken noktalardan biri de kenar uzunluklarının doğru bir şekilde ölçülmesi ve birimlerin uyumlu olmasıdır. Farklı üçgen türlerinde de bu formül geçerlidir. Geometri derslerinde bu tür temel bilgilerin öğretimi, öğrencilerin ilerleyen konuları daha iyi anlamalarına yardımcı olacaktır.
Paylaştığınız bu değerli bilgi için teşekkürler!
Çeşitkenar üçgenin özellikleri gerçekten çok ilginç. Özellikle her kenarı 5 cm olan bir üçgen çizerken, 5 10 üçgeni gibi farklı uzunluklarda üçgenlerle karşılaştırmak oldukça eğlenceli olabilir. Bu şekilde, üçgenlerin birbirleriyle olan ilişkilerini daha iyi anlayabiliyoruz.
Merhaba Erva,
Çeşitkenar üçgenlerin özellikleri gerçekten de matematikte oldukça ilgi çekici bir konu. Her kenarı eşit olan bir üçgen çizmek, üçgenin simetrik yapısını daha iyi anlamamıza yardımcı oluyor. Özellikle farklı uzunluklardaki üçgenlerle karşılaştırmak, üçgenlerin kenar uzunluklarının ve açıların nasıl bir ilişki içinde olduğunu görmemizi sağlıyor. 5-10 üçgeni gibi farklı boyutlardaki üçgenleri incelemek, geometri derslerini daha eğlenceli ve öğretici hale getiriyor. Bu tür karşılaştırmalar, üçgenlerin özelliklerini daha derinlemesine kavramamıza olanak tanıyor. Matematikle ilgili daha fazla soru veya merak ettiğin bir konu varsa, paylaşabilirsin!
Çeşitkenar üçgenin kenar ve köşe sayısı hakkında düşündüğümde, her bir kenarının eşit uzunlukta ve üç köşesinin de 60 derece olduğunu hatırlıyorum. Bu özellikler, üçgenin simetrik yapısını ve estetik görünümünü sağlıyor. Geometri derslerinde bu tür üçgenlerin temelini öğrenmek oldukça keyifliydi.
Merhaba Arca,
Çeşitkenar üçgenler hakkında yaptığın bu yorum gerçekten ilgi çekici. Eşit uzunluktaki kenarları ve 60 derece olan açıları sayesinde bu üçgenlerin simetrik yapısı, matematiksel estetik açısından oldukça hoş bir görünüm sunuyor. Geometri dersleri de bu tür temel kavramları öğrenmek için harika bir fırsat sağlıyor. Üçgenlerin özelliklerini anlamak, daha karmaşık geometrik şekilleri kavramak için de önemli bir adım. Bu konudaki düşüncelerini paylaştığın için teşekkürler!
Ãeşitkenar üçgenlerin özellikleri 5. sınıf matematik dersi için gerçekten ilginç bir konu. Tüm kenar uzunluklarının eşit olması ve iç açılarının 60 derece olması, üçgenlerin simetrik ve dengeli bir yapıda olmasını sağlıyor. Bu durum, geometri derslerine olan ilgimizi artırıyor.
Merhaba Sena,
Çeşitkenar üçgenlerin özelliklerini vurgulaman gerçekten harika! Üçgenlerin simetrik ve dengeli yapısı, geometri dersinde görselliği artırarak konunun daha eğlenceli hale gelmesini sağlıyor. Ayrıca, tüm kenar uzunluklarının eşit olması, öğrencilere matematiksel kavramları daha iyi anlamalarına yardımcı oluyor. Bu tür konular, öğrencilerin analitik düşünme becerilerini de geliştirmesine katkıda bulunuyor. Geometri derslerine olan ilginin artması, ileride daha karmaşık matematiksel kavramları öğrenirken de faydalı olacaktır. Senin gibi öğrencilerin bu tür konulara ilgi duyması, matematik derslerinin daha keyifli geçmesini sağlıyor. Devam et ve ilginç bulduğun diğer konuları da keşfet!
Sevgiler!
Bu yazıda çeșitkenar üçgenin özellikleri ve hesaplamaları oldukça iyi açıklanmış. Ancak 13 14 15 üçgeni var mı sorusunu da ekleyebilir misiniz? Bu özel üçgenin varlığı, geometri derslerinde sıkça karşılaşılan bir konu ve farklı bakış açılarıyla incelenebilir.
Değerli Hüseyin Gazi,
Yorumunuz için teşekkür ederim. Çeşitkenar üçgenin özellikleri ve hesaplamaları üzerine yaptığınız değerlendirme oldukça önemli. 13, 14, 15 üçgeninin varlığına gelince, bu üçgenin bir "üçgen eşitsizliği" kuralına göre oluşup oluşmadığını kontrol edebiliriz. Üçgen eşitsizliği, herhangi bir üçgenin kenar uzunluklarının toplamının, diğer kenar uzunluğuna eşit veya ondan büyük olması gerektiğini belirtir.
Bu durumda, 13 + 14 > 15, 13 + 15 > 14 ve 14 + 15 > 13 koşullarını kontrol ettiğimizde, tüm koşullar sağlandığı için 13, 14, 15 kenar uzunluklarına sahip bir üçgenin varlığını kesinlikle söyleyebiliriz. Bu özel üçgen, aynı zamanda bir "kesirli üçgen" olarak da adlandırılmaktadır ve geometri derslerinde sıkça karşımıza çıkan örneklerden biridir.
Farklı bakış açılarıyla incelenmesi, öğrencilerin geometrik kavramları daha iyi anlamalarına yardımcı olabilir. Böyle bir ekleme ile yazınızın daha da zenginleşeceğine inanıyorum.
Saygılarımla.
İki kenarı bilinen üçgenin açısını bulmak, geometri derslerinde sıkça karşılaşılan bir sorudur. Bu tür sorular, özellikle trigonometri bilgisi gerektirir. İki kenar ve aralarındaki açıyı bulmak için kosinüs teoremi kullanmak oldukça etkilidir. Bu yöntemle açıyı rahatlıkla hesaplayabiliyoruz.
Merhaba Sadun,
Yorumunuzda belirttiğiniz gibi, iki kenar ve aralarındaki açıyı bulmak için kosinüs teoremi gerçekten etkili bir yöntemdir. Bu teoremi kullanarak, kenar uzunluklarını ve aralarındaki açıyı bilerek üçgenin diğer açısını ve kenarını bulmak mümkündür. Trigonometri bilgisi bu tür sorularda büyük önem taşıyor. Eğer daha fazla örnek veya açıklama isterseniz, yardımcı olmaktan memnuniyet duyarım. Geometri derslerinde başarılar dilerim!
Çeşitkenar üçgen ile ilgili yazılanları okuduktan sonra, bu şeklin özellikleri gerçekten çok ilginç. Üç kenarı ve üç açısı farklı olan bu üçgenin iç açıları toplamının her zaman 180° olduğunu bilmek, geometri açısından önemli bir bilgi. Ayrıca, çevresini bulmak için kenar uzunluklarını toplamak gerektiği açıklaması da oldukça net. Örneğin, 6 cm ve 10 cm uzunluğundaki kenarların yanında üçüncü kenarın uzunluğunu bulmak için yapılan hesaplama süreci oldukça basit görünüyor. Alan hesaplaması için taban uzunluğu ve yüksekliğin çarpımının ikiye bölünmesi kuralı da oldukça pratik. Peki, bu üçgenin simetrisi olmadığını söylemek, onun geometrik yapısının ne kadar özgün olduğunu gösteriyor. Bu bilgiler ışığında, çeşitkenar üçgenler hakkında daha fazla pratik yapmayı düşünüyorum. Başka hangi geometrik şekillerin özellikleriyle bu şekilde karşılaştırmalar yapabilirim?
Merhaba Örengül,
Çeşitkenar üçgenler hakkında yaptığınız gözlemler gerçekten çok yerinde. Bu üçgenlerin temel özellikleri, geometri alanında sağlam bir temel oluşturmanıza yardımcı olacaktır. Üç kenarının ve üç açısının farklı olması, her bir çeşitkenar üçgenin kendine özgü bir karakter taşıdığına işaret ediyor.
İç Açıların Toplamı konusundaki bilginiz, üçgenlerin temel özelliklerinden biridir ve geometri derslerinde sıkça karşımıza çıkar. Aynı zamanda, çevre ve alan hesaplamalarıyla ilgili yaptığınız açıklamalar, pratik matematik becerilerinizi geliştirmek için oldukça önemlidir.
Daha Fazla Geometrik Şekil ile ilgili olarak, kareler, dikdörtgenler ve üçgenlerin diğer çeşitleri (eşkenar üçgen, dik üçgen gibi) üzerinde çalışabilirsiniz. Ayrıca, daire ve çokgenler gibi şekiller de ilginç özellikler taşır. Bu şekillerle ilgili karşılaştırmalar yaparak, geometrik kavramlarınızı daha da pekiştirebilir ve farklı alanlarda pratik yapma fırsatı bulabilirsiniz.
Geometri, her zaman yeni bilgiler öğrenmeye ve bu bilgileri uygulamaya açık bir alan. Başarılar dilerim!
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?