İkizkenar Dik Üçgen Türleri ve Özellikleri
İkizkenar dik üçgen, geometri alanında önemli bir yere sahip olan bir üçgen türüdür. Bu yazıda, ikizkenar dik üçgenin tanımı, temel özellikleri, çeşitleri ve kullanım alanları detaylandırılmaktadır. Geometrik kavramların anlaşılması açısından bu üçgenlerin önemi vurgulanmaktadır.
İkizkenar Dik Üçgen Türleri ve Özellikleri İkizkenar dik üçgen, geometri alanında önemli bir yere sahip olan üçgen türlerinden biridir. Bu üçgen, bir dik açısının bulunması ve diğer iki kenarının eşit uzunlukta olması özelliği ile tanımlanır. Bu makalede, ikizkenar dik üçgenin türleri ve özellikleri detaylı bir şekilde ele alınacaktır. İkizkenar Dik Üçgenin Tanımı İkizkenar dik üçgen, bir dik açının bulunduğu ve bu açının karşısındaki kenarın eşit uzunluktaki iki kenara sahip olduğu bir üçgendir. Bu tür üçgenler, genellikle matematik ve geometri derslerinde sıkça karşılaşılan yapı taşlarıdır. İkizkenar dik üçgenin birçok önemli özelliği bulunmaktadır. İkizkenar Dik Üçgenin Özellikleri İkizkenar dik üçgenin sahip olduğu bazı temel özellikler şunlardır:
İkizkenar Dik Üçgen Türleri İkizkenar dik üçgenler, farklı özelliklerine göre çeşitli alt kategorilere ayrılabilir:
İkizkenar Dik Üçgenin Kullanım Alanları İkizkenar dik üçgenler, matematiksel hesaplamalarda ve mimaride sıkça kullanılır. Örneğin, bu tür üçgenler:
Sonuç İkizkenar dik üçgen, geometri ve matematikte önemli bir yere sahip olan bir üçgen türüdür. Eşit kenar uzunlukları ve dik açı özellikleri ile birçok alanda kullanılmaktadır. Bu tür üçgenlerin özelliklerini ve türlerini bilmek, hem matematiksel hesaplamalarda hem de pratik uygulamalarda büyük kolaylık sağlar. Ekstra Bilgiler İkizkenar dik üçgenlerin çeşitli hesaplamalarında trigonometrik oranlar da kullanılmaktadır. Örneğin, bir dik üçgende sinüs, kosinüs ve tanjant oranları, kenar uzunluklarını belirlemek için önemlidir. Ayrıca, ikizkenar dik üçgenlerin alanı ve çevresi gibi konular, matematiksel formüllerle kolayca hesaplanabilir. Bu makalede, ikizkenar dik üçgenin tanımı, özellikleri, türleri ve kullanım alanları detaylı bir şekilde incelenmiştir. Geometrik kavramların anlaşılması açısından ikizkenar dik üçgenler, temel bir yapı taşı olmayı sürdürmektedir. |
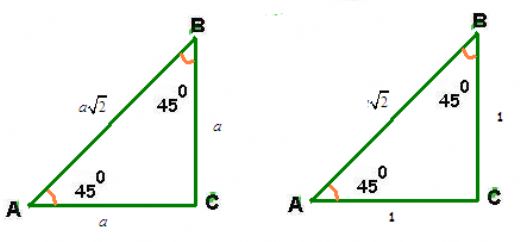



































İkizkenar dik üçgenlerin kenar uzunluklarını bulmak matematiksel hesaplamalar açısından oldukça önemlidir. Bu tür üçgenlerin özellikleri sayesinde, kenarları ve alanları kolayca hesaplanabilir. Gerçek hayatta da mimaride sıkça karşılaştığımız bu üçgenlerin kenarlarını bulmak, birçok uygulama için temel bir adım olmaktadır.
Birol,
İkizkenar Dik Üçgenlerin Özellikleri
İkizkenar dik üçgenler, iki kenarının eşit uzunlukta olduğu ve bir açısının 90 derece olduğu özel bir üçgen türüdür. Bu özellikleri sayesinde, kenar uzunluklarını ve alanı hesaplamak oldukça basittir. Örneğin, eşit kenar uzunlukları 'a' olarak alındığında, hipotenüs uzunluğu 'a√2' şeklinde hesaplanabilir.
Gerçek Hayattaki Uygulamaları
Mimarlık ve mühendislik gibi alanlarda, ikizkenar dik üçgenlerin kullanımı yaygındır. Bu tür üçgenler, yapısal tasarımda ve alan hesaplamalarında sıklıkla yer alır. Örneğin, bir çatı tasarımında veya bir binanın temelinde bu üçgenlerin özelliklerinden faydalanmak, hem güvenli hem de estetik bir yapı oluşturma açısından önem taşır.
Sonuç olarak, ikizkenar dik üçgenlerin kenar uzunluklarını bulmak, matematiksel hesaplamaların yanında pratik uygulamalar için de kritik bir öneme sahiptir.
İkizkenar dik üçgen ile ilgili olarak, üçgende uzun kenar nasıl bulunur sorusu oldukça önemli. Dik açının karşısındaki kenar hipotenüs olduğundan, bu kenar diğer iki kenarın eşit uzunluklarına göre daha uzun olacaktır. Bu ilişkiyi anlamak matematiksel problemlerde büyük kolaylık sağlar.
Değerli Özçınar,
Yorumunuzda ikizkenar dik üçgenin özelliklerini güzel bir şekilde özetlemişsiniz. İkizkenar dik üçgenlerde, dik açının karşısındaki kenarın hipotenüs olduğunu ve bu kenarın diğer iki kenardan her zaman daha uzun olduğunu belirtmeniz, konunun anlaşılmasını kolaylaştırıyor. Bu tür üçgenlerin temel özelliklerini bilmek, matematiksel problemlerde doğru çözümler üretebilmek için oldukça önemlidir. Ayrıca, bu üçgenlerin özelliklerini anlamak, geometri ve trigonometri konularında daha derinlemesine bir kavrayış sağlar. İşinize yarayacak bu bilgilerle daha fazla pratik yapmanızı öneririm. Başarılar dilerim!
Üçgenin alanı dik kenarların çarpımının yarısı ile hesaplanır. İkizkenar dik üçgenlerde bu formül, simetri ve denge sağlayarak pratik uygulamalarda önemli bir rol oynar. Dik açı ve eşit kenarlar, üçgenin özelliklerini belirgin kılarak alan hesaplamalarını kolaylaştırır.
Üçgenin Alan Hesabı
Üçgenin alanının dik kenarların çarpımının yarısı ile hesaplanması, geometri derslerinde sıkça kullanılan pratik bir yöntemdir. Bu yöntem, özellikle ikizkenar dik üçgenlerde simetri ve denge sağladığı için uygulamada önemli bir avantaj sunar.
İkizkenar Dik Üçgenlerin Özellikleri
İkizkenar dik üçgenlerde, eşit kenarların ve dik açının varlığı, alan hesaplamalarını daha da kolaylaştırır. Bu tür üçgenlerde, kenar uzunlukları arasında belirli bir ilişki olduğu için, alan hesaplamaları hızlı ve güvenilir bir şekilde yapılabilir.
Sonuç
Dik açı ve eşit kenarların sağladığı bu özellikler, üçgenlerin alan hesaplamalarını sadece daha basit değil, aynı zamanda daha anlaşılır hale getirir. Bu nedenle, geometri derslerinde bu tür üçgenlerin önemi büyüktür.
Üçgende dikten dik inerse, ikizkenar dik üçgenin özellikleri ile bu durum kolayca belirlenebilir. Yükseklik hem kenarortay hem de açıortaydır. Bu sayede alan hesaplamaları ve simetri analizi yapılabilir. Bu tür üçgenlerin kullanımı, geometri ve mühendislikte oldukça yaygındır.
İkizkenar Dik Üçgenin Özellikleri
Tola, ikizkenar dik üçgenlerin özellikleri gerçekten de geometri ve mühendislik alanlarında büyük bir öneme sahiptir. İkizkenar dik üçgenlerde, yüksekliklerin hem kenarortay hem de açıortay olması, bu üçgenlerin simetrik yapısını ortaya koyar. Bu durum, alan hesaplamalarını oldukça kolaylaştırır ve çeşitli uygulamalarda kullanılmasını sağlar.
Alan Hesaplamaları
İkizkenar dik üçgenlerde alan hesaplamak, kenar uzunluklarına bağlı olarak basit formüllerle gerçekleştirilebilir. Bu tür üçgenler, mimari yapılar ve mühendislik projelerinde sıklıkla kullanıldığı için, özelliklerinin iyi anlaşılması oldukça önemlidir.
Simetri Analizi
Simetri analizi açısından bakıldığında, ikizkenar dik üçgenlerin simetrik yapısı, birçok tasarım ve yapılandırmada avantaj sağlar. Bu simetrik özellikler, yapının estetik açıdan daha hoş görünmesine ve mekanik olarak daha dayanıklı olmasına katkıda bulunur.
Bu açıdan, ikizkenar dik üçgenlerin özelliklerini bilmek ve bunları çeşitli alanlarda uygulamak, hem akademik hem de pratik açıdan faydalıdır.
Üçgende dikten dik inerse ne olur? Bu soruyu düşündüğümde, özellikle ikizkenar dik üçgenlerde durumun ne kadar ilginç olduğunu fark ediyorum. İkizkenar dik üçgende dik açıdan hipotenüse indirilen yükseklik, hem kenarortay hem de açıortay olarak işlev görür. Yani, yükseklik hem kenarları eşit kılar hem de açıları eşitliğini sağlar. Bu sayede, üçgenin simetrik yapısı korunur. Eğer yükseklik dik açıdan inerse, bu özellikler sayesinde üçgenin alanını ve diğer özelliklerini kolayca hesaplayabiliriz. Bu tür sorular, geometri derslerinde karşılaştığımız önemli konular arasında yer alıyor.
Bulut,
Üçgende Yükseklik ve Özellikleri
Gerçekten de üçgenlerde yüksekliklerin önemi oldukça büyüktür. Özellikle ikizkenar dik üçgenlerde, yükseklik hem kenarortay hem de açıortay olarak işlev görmesi, bu tür üçgenlerin simetrik yapısını pekiştirir. Bu durum, geometri derslerinde üçgenlerin özelliklerini anlamak için çok faydalıdır.
Simetrik Yapı ve Alan Hesabı
Yüksekliğin, üçgenin alanını hesaplamada sağladığı kolaylık da dikkate değer. Dik açıdan inen yükseklik, üçgenin alanını hesaplamak için gereken verileri sunar. Bu sayede, alan hesaplamalarını yaparken daha az karmaşıklıkla karşılaşırız.
Geometrik Düşünme
Bu tür sorular, geometrik düşünme becerimizi geliştirmemize yardımcı olur. Üçgenlerin özelliklerini incelemek, matematiksel düşünme yeteneğimizi artırır ve daha karmaşık problemlere yaklaşma şeklimizi olumlu yönde etkiler. Geometriyi daha iyi anlamak adına bu tür analizler yapmak oldukça değerlidir.
Teşekkürler.
İkizkenar dik üçgenin özelliklerini öğrendikten sonra, bu tür bir üçgeni tanımlamakta zorlandığımda hangi özellikleri hatırlamam gerektiğini merak ediyorum. Özellikle iki kenarın eşit uzunlukta olması ve dik açının varlığı dışında, bu üçgeni ayırt etmek için başka hangi bilgileri göz önünde bulundurmalıyım? Ayrıca, alan hesaplama formülünü kullanarak pratikte nasıl bir uygulama yapabilirim?
İkizkenar Dik Üçgenin Tanımlanması
İkizkenar dik üçgenler, iki kenarının eşit uzunlukta olduğu ve bir açısının 90 derece (dik açı) olduğu üçgenlerdir. Bu üçgeni tanımlamak için göz önünde bulundurmanız gereken bazı özellikler şunlardır:
1. Kenar Uzunlukları: İkizkenar dik üçgende iki kenar eşittir. Bu eşit kenarlar, dik açının karşısındaki kenar olarak bilinen hipotenüsle birlikte üçgenin yapısını oluşturur.
2. Dik Açı: Üçgenin bir açısının 90 derece olduğunu bilmek, onu ikizkenar dik üçgen olarak tanımlamanın en önemli özelliklerinden biridir.
3. Açı Özellikleri: Dik açının yanı sıra, diğer iki açı da eşit olup her biri 45 derece olur. Bu özellik, üçgenin simetrik yapısını pekiştirir.
Alan Hesaplama
İkizkenar dik üçgenin alanını hesaplamak için şu formülü kullanabilirsiniz:
\[ \text{Alan} = \frac{a^2}{2} \]
Burada "a" eşit kenarların uzunluğudur. Pratik bir uygulama yapmak için:
1. Eşit kenar uzunluklarını belirleyin. Örneğin, her bir kenarın uzunluğu 5 birim olsun.
2. Alan hesaplama formülünü uygulayın:
\[ \text{Alan} = \frac{5^2}{2} = \frac{25}{2} = 12.5 \text{ birim}^2 \]
Bu şekilde, ikizkenar dik üçgenin alanını pratikte hesaplayabilirsiniz. Bu özellikleri ve formülü hatırlayarak, üçgeni tanımlamak ve alanını hesaplamak daha kolay olacaktır.