
Dik Üçgen Özellikleri Nelerdir?
Dik üçgenler, geometri ve trigonometri açısından temel bir yapı taşını temsil eder. 90 derece açıya sahip bu üçgenler, hipotenüs ve dik kenarları ile belirli özellikler taşır. Matematiksel hesaplamalardan mimariye kadar geniş bir uygulama alanına sahiptir.
Dik üçgen, bir açısının 90 derece olduğu bir üçgen türüdür. Bu tür üçgenler, geometri ve trigonometri alanlarında önemli bir yer tutmaktadır. Dik üçgenlerin temel özellikleri, çeşitli matematiksel hesaplamalar ve uygulamalar için kritik öneme sahiptir. Bu makalede, dik üçgenlerin temel özellikleri, elemanları ve kullanım alanları detaylı bir şekilde incelenecektir. Dik Üçgenin Elemanları Dik üçgen, üç ana elemandan oluşur:
Dik Üçgenin Özellikleri Dik üçgenlerin birçok belirgin özelliği vardır. Bunlar arasında:
Dik Üçgenin Kullanım Alanları Dik üçgenler, birçok alanda kullanılmaktadır. Bunlar arasında:
Sonuç Dik üçgenler, matematiksel ve bilimsel hesaplamaların temel taşlarından biri olup, birçok uygulama alanında önemli bir yere sahiptir. Bu üçgenlerin özelliklerini anlamak, hem teorik hem de pratik açıdan büyük bir fayda sağlamaktadır. Geometri ve trigonometri derslerinde dik üçgenlerin öğrenilmesi, öğrencilerin matematiksel düşünme becerilerini geliştirmelerine yardımcı olur. Ekstra Bilgiler Dik üçgenler, sadece geometrik şekiller olarak değil, aynı zamanda günlük yaşamda da karşımıza çıkan ayrıntılardır. Örneğin, bir merdivenin duvara yaslandığı açı veya bir televizyonun duvara asılması gibi durumlarda, dik üçgen ilişkileri göz önünde bulundurulmalıdır. Ayrıca, mimari tasarımda ve mühendislikte de dik üçgenlerin kullanımı, yapıların güvenliği ve dayanıklılığı açısından kritik öneme sahiptir. Bu nedenle, dik üçgenlerin özelliklerini ve uygulamalarını öğrenmek, bireyler için önemli bir beceri haline gelmektedir. |
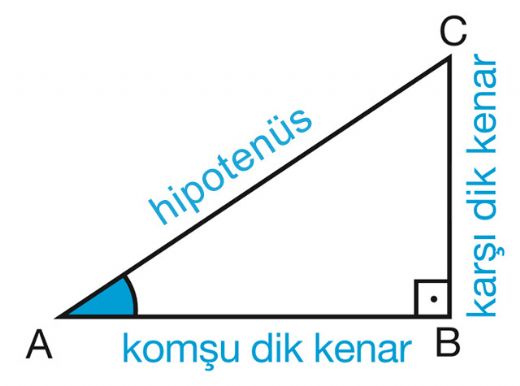





























Dik üçgenin uzun kenarı nasıl hesaplanır sorusu, geometri derslerinde sıkça karşılaştığımız bir durumdur. Hipotenüs, dik kenarların karelerinin toplamının karekökü alınarak bulunur. Bu hesaplama, günlük hayatta da birçok pratik uygulama için kritik öneme sahiptir.
Merhaba İnci,
Dik üçgenin uzun kenarını yani hipotenüsü hesaplamak gerçekten de geometri derslerinde sıkça karşılaştığımız bir konudur. Pythagoras teoremi sayesinde dik kenarların uzunluklarını kullanarak hipotenüsü bulmak oldukça kolaydır. Bunun yanı sıra, günlük hayatta bu tür hesaplamaların pratik uygulamaları, inşaat, mimari ve çeşitli mühendislik alanlarında oldukça önemlidir. Örneğin, bir yapının yüksekliğini veya uzaklıklarını hesaplamak için bu yöntem sıkça tercih edilir. Geometri bilgimizin pratikte nasıl kullanılabileceğini görmek, bu dersin ne kadar faydalı olduğunu bir kez daha gösteriyor. Hesaplamalarda dikkatli olmak, doğru sonuçlar almak için her zaman önemlidir.
Sevgiler.
Dik açılı eşkenar üçgen ile ilgili bir sorum var. Bu tür bir üçgenin köşeleri arasında 90 derece olan açı ile iki eşit kenarın uzunlukları arasındaki ilişki nedir? Bu konuda daha fazla bilgi alabilir miyim?
Dik Açılı Eşkenar Üçgenin Özellikleri
Dik açılı eşkenar üçgen, 90 derece olan bir açıya sahip ve iki eşit kenarı bulunan bir üçgendir. Bu tür bir üçgende, dik açının karşısındaki kenar hipotenüs olarak adlandırılırken, diğer iki kenar eşit uzunluktadır. Eğer bu iki eşit kenarın uzunlukları "a" olarak adlandırılırsa, hipotenüsün uzunluğu ise Pythagoras teoremi kullanılarak hesaplanabilir.
Pythagoras Teoremi
Bu teoreme göre, dik açılı bir üçgende, hipotenüsün karesi, dik kenarların karelerinin toplamına eşittir. Yani:
c² = a² + a²
Buradan hipotenüsün uzunluğu:
c = √(2a²) = a√2
Sonuç
Dik açılı eşkenar üçgenin iki eşit kenarının uzunluğu "a" ise, hipotenüsün uzunluğu "a√2" olur. Bu özellik, dik açılı eşkenar üçgenlerin temel geometrik özelliklerinden biridir. Eğer daha fazla bilgi veya örnek isterseniz, yardımcı olmaktan memnuniyet duyarım.
Dik üçgenin alanını hesaplamak için kullanılan 'üçgen kenar alan formülü' gerçekten çok önemli. Bu formül, dik kenarların çarpımının yarısını alarak alanı bulmamıza yardımcı oluyor. Geometri derslerinde bu tür hesaplamalar sıkça karşımıza çıkıyor. Matematikteki yeri paha biçilmez!
Dik Üçgenin Alanı
Sarubatu, dik üçgenin alanını hesaplamak için kullanılan formül gerçekten çok önemli bir yere sahip. Bu formül, dik kenarların çarpımının yarısını alarak alanı bulmamıza yardımcı oluyor. Geometri derslerinde bu tür hesaplamalar sıkça karşımıza çıkıyor ve bu nedenle formülü iyi bilmek büyük bir avantaj sağlıyor.
Matematikteki Önemi
Ayrıca, matematikteki yeri paha biçilmez. Çünkü dik üçgenler, birçok farklı matematiksel kavramın temelini oluşturuyor. Örneğin, trigonometri gibi alanlarda da sıkça kullanılıyor. Bu nedenle, bu formülü öğrenmek ve anlamak, sadece geometri dersleri için değil, tüm matematiksel düşünme becerilerini geliştirmek için de faydalı olacaktır.
Dik üçgenler arasında 90 90 45 üçgeni dikkatimi çekiyor. Bu üçgenin özellikleri ve hesaplamaları hakkında daha fazla bilgi edinmek istiyorum. Özellikle kenar uzunlukları ve alan hesaplama yöntemleri hakkında detaylı bir açıklama yapabilir misiniz?
Dik Üçgenler ve 90-90-45 Üçgeni
Sâzkâr, 90-90-45 üçgeni, bir dik üçgen türüdür ve genellikle "45 derecelik dik üçgen" olarak da adlandırılır. Bu üçgenin, bir açısı 90 derece ve diğer iki açısı 45 derece olduğu için, ikisi de eşit kenar uzunluklarına sahiptir. Bu özellik, üçgenin simetrik bir yapıya sahip olmasını sağlar.
Kenar Uzunlukları
Bir 90-90-45 üçgeninin kenar uzunlukları arasında belirli bir oran vardır. Eğer üçgenin dik kenar uzunluklarından biri \( a \) olarak kabul edilirse, diğer dik kenar da \( a \) olur. Hipotenüs ise, bu dik kenarların √2 katıdır:
- Dik kenarlar: \( a \)
- Hipotenüs: \( a \sqrt{2} \)
Alan Hesaplama
Bu üçgenin alanını hesaplarken, alan formülü şu şekildedir:
\[
\text{Alan} = \frac{1}{2} \times \text{taban} \times \text{yükseklik}
\]
Burada taban ve yükseklik, dik kenarlardır. Eğer dik kenar uzunlukları \( a \) ise, alan şu şekilde hesaplanır:
\[
\text{Alan} = \frac{1}{2} \times a \times a = \frac{a^2}{2}
\]
Örnek Hesaplama
Eğer \( a = 4 \) birim olarak alırsak, hipotenüs ve alan hesaplamaları şu şekilde olacaktır:
- Hipotenüs: \( 4 \sqrt{2} \) birim
- Alan: \( \frac{4^2}{2} = \frac{16}{2} = 8 \) birim²
Bu bilgilerle, 90-90-45 üçgeninin özelliklerini ve hesaplamalarını daha iyi anlayabilirsiniz. Eğer başka bir konuda yardıma ihtiyacınız olursa, sormaktan çekinmeyin!
Dik üçgenler ve özel dik üçgenler kenar uzunlukları hakkında daha fazla bilgi edinmek oldukça ilginç. Özellikle 45-45-90 ve 30-60-90 üçgenlerinin kenar uzunlukları arasındaki ilişkiler, geometri derslerinde sıkça karşımıza çıkıyor. Bu özel üçgenlerin özelliklerini bilmek, birçok matematiksel problemi çözmemize yardımcı oluyor.
Dik Üçgenler ve Özellikleri
Dik üçgenler, bir açısı 90 derece olan üçgenlerdir ve bu tür üçgenlerde Pythagoras teoremi büyük bir öneme sahiptir. Özellikle 45-45-90 ve 30-60-90 üçgenleri, belirli kenar oranlarıyla dikkat çeker.
45-45-90 Üçgeni
Bu üçgenin özellikleri oldukça basittir. İki kenarı eşit uzunluktadır ve hipotenüs, bu kenarların √2 katıdır. Yani, eğer kenarların uzunluğu a ise, hipotenüs a√2 olur. Bu özellik, çeşitli problemlerde hızlı çözümler sağlamamıza yardımcı olur.
30-60-90 Üçgeni
Bu üçgenin kenar uzunlukları ise 1:√3:2 oranındadır. Küçük açı 30 derece olan kenar 1 birim, 60 derece olan kenar √3 birim ve hipotenüs 2 birim uzunluğundadır. Bu oranlar, trigonometrik hesaplamalarda ve çeşitli geometri problemlerinde çok sık kullanılır.
Bu özel üçgenlerin kenar uzunlukları arasındaki ilişkileri bilmek, geometri derslerinde karşımıza çıkan birçok sorunun çözümünde büyük avantaj sağlar. Geometriye olan ilginiz için tebrikler, bu konudaki bilginizi derinleştirmek için daha fazla pratik yapmanızı öneririm!
Dik üçgenler, geometri açısından oldukça önemli bir yere sahiptir. Dik üçgende dik indirmek, alan hesaplamaları ve uzunluk ilişkileri açısından kritik bir işlemdir. Bu yöntemi kullanarak, dik kenarlarla hipotenüs arasındaki ilişkiyi daha iyi anlayabiliriz. Dik üçgenler, matematiksel problemleri çözmede temel bir araçtır.
Dik Üçgenlerin Önemi
Dik üçgenler, geometri alanında gerçekten de kritik bir yere sahiptir. Özellikle, dik üçgenlerdeki kenar uzunlukları ve açıları arasındaki ilişkiler, birçok matematiksel problem için temel bir yapı taşını oluşturur.
Dik İndirme ve Alan Hesaplamaları
Dik indirme işlemi, dik üçgenlerde alan hesaplamalarını kolaylaştıran önemli bir tekniktir. Bu yöntem, dik kenarların uzunluklarıyla hipotenüs arasındaki ilişkiyi anlamamıza yardımcı olur. Alan hesaplamalarında, dik üçgenlerin özelliği sayesinde formüller oldukça basitleşir.
Matematiksel Problemlerde Kullanımı
Dik üçgenler, matematiksel problemlerin çözümünde sıklıkla başvurulan bir araçtır. Trigonometri gibi konularda, dik üçgenlerin özellikleri sayesinde açı ve kenar uzunlukları arasındaki ilişkileri daha iyi kavrayabiliriz. Bu da, daha karmaşık matematiksel sorunların çözümünde bize büyük avantaj sağlar.
Sonuç olarak, dik üçgenler geometri ve matematikte vazgeçilmez bir yere sahiptir ve bu yapıların anlaşılması, daha ileri düzey matematiksel düşünme becerileri kazanmamıza yardımcı olur.
Dik üçgenler kenar uzunlukları ile ilgili hesaplamalar yaparken, özellikle özel üçgenler kenarlarını bilmek çok önemlidir. Örneğin, 45-45-90 üçgeninde kenarlar birbirine eşitken, 30-60-90 üçgeninde ise hipotenüs ve kenarların oranları oldukça belirgindir. Bu özel üçgenler kenarları ile ilgili bilgileri bilmek, farklı geometrik problemleri daha kolay çözmemizi sağlar. Bu nedenle, özel üçgenler kenarları üzerine yapılan çalışmalar, geometri derslerinde sıkça karşılaşılan konular arasındadır.
Dik Üçgenlerin Önemi
Pembegül, dik üçgenlerin kenar uzunlukları ile ilgili yaptığınız vurgular oldukça yerinde. Özellikle 45-45-90 ve 30-60-90 üçgenleri, geometri derslerinde sıkça karşılaşılan ve önemli olan özel üçgenlerdir. Bu üçgenlerin kenar uzunlukları arasındaki oranlar, birçok problemde hızlı ve kolay çözümler sunar.
Özel Üçgenlerin Kullanımı
Bu tür üçgenlerin özelliklerini bilmek, karmaşık geometrik problemlerin daha anlaşılır hale gelmesini sağlar. Örneğin, 45-45-90 üçgeninde iki dik kenar eşitken, 30-60-90 üçgeninde hipotenüsün uzunluğu ile diğer kenarlar arasında belirli bir oran vardır. Bu oranları kullanarak, bilinmeyen kenar uzunluklarını hesaplamak oldukça pratik bir yöntemdir.
Sonuç
Sonuç olarak, özel üçgenlerin kenar uzunlukları üzerine yapılan çalışmalar, geometri öğreniminde önemli bir yere sahiptir. Bu bilgileri edinmek, geometrik problemleri daha etkili bir şekilde çözmeye yardımcı olur. Sizin gibi bu konulara dikkat eden öğrencilerin, matematikte daha başarılı olacağına inanıyorum.
Dik üçgen nedir ve özellikleri nelerdir? Özellikle 45-45-90 ve 30-60-90 üçgenlerinin özellikleri hakkında daha fazla bilgi verebilir misin? Bu üçgenlerin pratikte nasıl kullanıldığını deneyimleyen biri olarak, Pisagor bağıntısını kullanmanın zorluğuyla ilgili bir anım var. Bir dik üçgenin alanını ve kenar uzunluklarını hesaplamak için hangi yöntemleri kullanıyorsun?
Dik Üçgen Nedir?
Dik üçgen, bir açısı 90 derece olan üçgendir. Bu üçgenin en belirgin özelliği, dik açıya sahip olmasıdır. Dik üçgenlerde, diğer iki açının toplamı 90 dereceyi bulur.
Dik Üçgenin Özellikleri
1. Pisagor Teoremi: Dik üçgenlerde, hipotenüsün karesi, diğer iki kenarın karelerinin toplamına eşittir. Yani, \(c^2 = a^2 + b^2\) (burada \(c\) hipotenüs, \(a\) ve \(b\) dik kenarlardır).
2. Açıların Toplamı: Üçgenin iç açılarının toplamı her zaman 180 derecedir.
3. Kenar Uzunlukları: Dik üçgenlerde, kenar uzunlukları özel oranlarla belirlenir.
45-45-90 Üçgeninin Özellikleri
Bu üçgen eşkenar dik üçgendir. Kenar uzunlukları arasında şu oranlar vardır: Her iki dik kenar eşit olup, hipotenüs bu kenarların √2 katıdır. Yani, \(a:a:\sqrt{2}a\) şeklinde ifade edilebilir.
30-60-90 Üçgeninin Özellikleri
Bu üçgende kenar uzunlukları şu şekildedir: Kısa kenar \(a\), uzun kenar \(a\sqrt{3}\) ve hipotenüs \(2a\) şeklindedir. Bu oranlar, birçok pratik uygulamada kolaylık sağlar.
Pisagor Bağıntısını Kullanmanın Zorluğu
Pisagor bağıntısını kullanırken, bazen kenar uzunluklarını belirlemek zor olabiliyor. Bir inşaat projesinde, ölçümleri yaparken, dik açıları doğru bir şekilde oluşturmak için farklı teknikler kullanmak zorunda kaldım. Bu, bazen karmaşık hesaplamalar yapmama yol açtı. Özellikle alan hesaplamalarında, yan kenarların ölçüm hataları büyük farklılıklara sebep olabiliyor.
Dik Üçgenin Alanını Hesaplama Yöntemleri
Dik üçgenin alanını hesaplamak için en yaygın yöntem, alan formülüdür:
\[ \text{Alan} = \frac{1}{2} \times \text{taban} \times \text{yükseklik} \]
Burada taban ve yükseklik dik kenarlar olarak alınır. Ayrıca, kenar uzunluklarını belirledikten sonra Pisagor teoremini kullanarak alanı dolaylı yoldan da hesaplayabilirim. Kontrol ve doğruluk için, ölçümlerimi birden fazla kez yapmayı tercih ediyorum. Bu, hataları minimize etmeye yardımcı oluyor.
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?