
Özel Üçgenler Nelerdir?
Özel üçgenler, belirli kenar uzunlukları ve açı ölçüleri ile tanımlanan geometrik şekillerdir. Eşkenar, ikizkenar ve dik üçgenler gibi türleri, matematikte ve çeşitli uygulamalarda önemli bir rol oynar. Bu yazıda, bu üçgenlerin özellikleri ve kullanım alanları ele alınmaktadır.
Özel üçgenler, bazı kenar uzunlukları ve açı ölçüleri ile karakterize edilen ve belirli matematiksel özellikler taşıyan üçgenlerdir. Bu üçgenler, geometri alanında önemli bir yer tutar ve çeşitli uygulamalarda sıkça kullanılır. Bu makalede, en bilinen özel üçgen türleri olan eşkenar, ikizkenar ve dik üçgenler ele alınacaktır. Eşkenar ÜçgenEşkenar üçgen, üç kenarı ve üç açısı da eşit olan bir üçgen türüdür. Bu tür üçgenlerde:
Eşkenar üçgenler, simetrik yapıları nedeniyle birçok matematiksel ve mimari uygulamada tercih edilmektedir. Ayrıca, eşkenar üçgenlerin alanı, kenar uzunluğuna bağlı olarak aşağıdaki formül ile hesaplanabilir: Alan = (√3/4) (kenar uzunluğu)² İkizkenar Üçgen İkizkenar üçgen, iki kenarı eşit uzunlukta olan ve buna bağlı olarak iki açısı da eşit olan bir üçgen türüdür. İkizkenar üçgenler ile ilgili bazı özellikler şunlardır:
İkizkenar üçgenler, çeşitli simetri özellikleri taşır ve bu nedenle sanatta ve doğada sıkça rastlanır. Dik Üçgen Dik üçgen, bir açısı 90 derece olan üçgendir. Dik üçgenlerin en önemli özelliği, Pythagoras Teoremi'ni sağlamasıdır. Bu teorem, dik üçgenin iki dik kenarının karelerinin toplamının, hipotenüsün karesine eşit olduğunu ifade eder:a² + b² = c²burada a ve b dik kenarları, c ise hipotenüstür. Dik üçgenlerle ilgili diğer önemli noktalar şunlardır:
Dik üçgenler, mühendislik, mimarlık ve birçok bilimsel alanda kullanılan temel geometrik şekillerdir. Özel Üçgenlerin Kullanım Alanları Özel üçgenler, matematiksel hesaplamalardan mimari tasarımlara kadar birçok alanda kullanılmaktadır. Özellikle:
Sonuç Özel üçgenler, geometri alanında temel yapı taşlarıdır ve birçok matematiksel özelliğe sahiptir. Eşkenar, ikizkenar ve dik üçgenler gibi farklı türleri, çeşitli alanlarda önemli uygulamalara sahiptir. Bu üçgenlerin incelenmesi, hem teorik hem de pratik açıdan büyük bir önem taşımaktadır. Özel üçgenlerin özelliklerini anlamak, matematiksel düşünmeyi geliştirmek ve gerçek dünya problemlerini çözmek için kritik bir adımdır. |
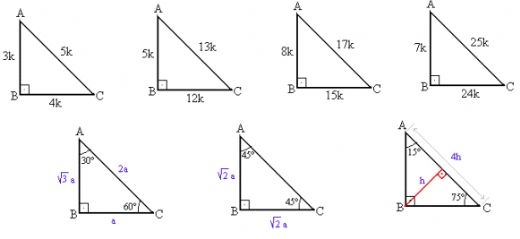















































Dik üçgenlerin özelliklerini anlamak için Pisagor bağıntısını nasıl kullanabilirim? Özellikle 3-4-5 üçgeni gibi özel üçgenlerde bu bağıntının nasıl uygulandığını örneklerle açıklayabilir misiniz?
Pisagor Bağıntısı:
Telvin, dik üçgenlerin özelliklerini anlamak için Pisagor bağıntısını kullanmak oldukça etkilidir. Pisagor bağıntısı, bir dik üçgende dik kenarların karelerinin toplamının hipotenüsün karesine eşit olduğunu ifade eder. Matematiksel olarak bu, \(a^2 + b^2 = c^2\) şeklinde yazılır. Burada \(a\) ve \(b\) dik kenarları, \(c\) ise hipotenüsü temsil eder.
3-4-5 Üçgeni Örneği:
3-4-5 üçgeni, Pisagor bağıntısının sıkça kullanılan özel bir örneğidir. Bu tip bir üçgende kenar uzunlukları sırasıyla 3, 4 ve 5 birimdir. Bu üçgeni Pisagor bağıntısıyla inceleyelim:
- Dik kenarlardan biri \(a = 3\) ve diğeri \(b = 4\) olarak alınır.
- Hipotenüs \(c = 5\) olur.
Pisagor bağıntısını uygulayarak kontrol edelim:
\[ 3^2 + 4^2 = 5^2 \]
\[ 9 + 16 = 25 \]
\[ 25 = 25 \]
Gördüğün gibi, bağıntı sağlanmaktadır. Bu örnek, Pisagor teoreminin doğruluğunu ve dik üçgenlerde nasıl kullanılacağını açıkça gösterir. Diğer dik üçgenlerde de aynı yöntemi uygulayarak kenar uzunluklarını bulabilirsin. Bu bağıntı, üçgenin herhangi iki kenarını bildiğinde üçüncü kenarı hesaplamanı sağlar ve dik üçgenlerin özelliklerini anlamanı kolaylaştırır.