
Üçgenin Açılımı ve Çeşitleri
Üçgen, geometri ve trigonometrinin temel unsurlarından biridir. Üçgenlerin açıları, kenar uzunlukları ve çeşitleri üzerine yapılan incelemeler, matematiğin birçok alanında önemli bir yere sahiptir. Bu yapıların özellikleri ve alan hesaplamaları, pratik uygulamalarla birleşerek mühendislikten mimariye kadar geniş bir yelpazede kullanılmaktadır.
Üçgenin Açılımı ve Çeşitleri Üçgen, üç kenarı ve üç açısı olan geometrik bir şekildir. Matematiksel olarak, üçgenler, geometri ve trigonometri alanlarında temel bir rol oynamaktadır. Üçgenin açılımı, bu şeklin kenarlarının ve açıların özelliklerini anlamak ve çeşitli üçgen türlerinin tanımlanmasını içerir. Bu yazıda, üçgenin açılımı, çeşitleri, özellikleri ve üçgenlerin uygulama alanları üzerinde durulacaktır. Üçgenin Temel Özellikleri Üçgenler, birçok temel özelliğe sahiptir. Bu özellikler arasında şunlar bulunmaktadır:
Üçgen Çeşitleri Üçgenler, kenar uzunluklarına ve açı ölçülerine göre farklı türlere ayrılmaktadır. Bu türler şu şekildedir:
Üçgenlerin Alan Hesabı Üçgenlerin alanını hesaplamak için genel olarak kullanılan formül, taban ve yükseklik kullanılarak hesaplanan alandır:\[ \text{Alan} = \frac{1}{2} \times \text{Taban} \times \text{Yükseklik} \]Bunun yanı sıra, kenar uzunluklarının bilindiği durumlarda Heron formülü de kullanılabilir:\[ s = \frac{a + b + c}{2} \]\[ \text{Alan} = \sqrt{s(s-a) (s-b) (s-c)} \]Burada \( a, b, c \) üçgenin kenar uzunluklarıdır ve \( s \) yarı çevreyi temsil etmektedir. Üçgenlerin Uygulama Alanları Üçgenler, matematikte ve mühendislikte birçok uygulama alanına sahiptir. Bunlar arasında:
Sonuç Üçgen, temel geometrik şekillerden biri olarak, açılar ve kenarlar arasındaki ilişkileri anlamamıza yardımcı olur. Üçgenlerin çeşitleri, özellikleri ve alan hesaplamaları, matematiğin ve mühendisliğin birçok alanında büyük öneme sahiptir. Üçgenlerin bu temel özellikleri ve uygulama alanları, onları hem teorik hem de pratik açıdan önemli kılar. Geometrik şekillerin anlaşılmasında ve çeşitli hesaplamalarda üçgenlerin rolü, matematiksel düşüncenin gelişimine katkıda bulunmaktadır. |
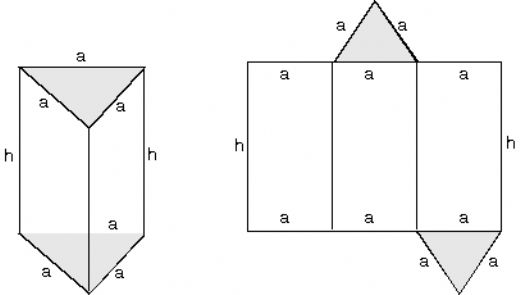





























Üçgen prizma açılımı ile ilgili bir soru sorarken, üçgenin temel özelliklerini ve alan hesaplamasını dikkate almak önemli. Üçgen prizmanın yüzey alanını bulmak için üçgenin alanını ve yan yüzeylerini hesaplamak gerekecek. Bu tür sorular matematiksel düşünme yeteneğimizi geliştirmekte.
Merhaba Özgür Deniz,
Yorumunuzda üçgen prizma konusunu ele almanız oldukça önemli. Üçgenin temel özellikleri ve alan hesaplamaları, üçgen prizmanın yüzey alanını bulma sürecinde kritik bir rol oynuyor. Özellikle üçgenin alanını bulurken, kenar uzunluklarını ve yükseklik değerlerini doğru kullanmak gerekir.
Yüzey Alanı Hesaplama kısmında ise, üçgenin alanını bulduktan sonra, yan yüzeylerin alanlarını da eklemek gerektiğini belirtiyorsunuz. Bu yaklaşım, matematiksel düşünme yeteneğimizi gerçekten geliştirmekte ve uzamsal düşünme becerilerimizi artırmakta. Böylece hem teorik bilgimizi pekiştiriyor hem de pratikte daha iyi kavrayabiliyoruz.
Bu konuda daha fazla örnek ya da pratik yapmak isterseniz, her zaman yardımcı olmaktan mutluluk duyarım. Başarılar dilerim!
Üçgenin açılımı hakkında daha fazla bilgi edinmek istiyorum. Özellikle üçgen çeşitlerinin açıları nasıl etkilediğini ve her bir türün hangi durumlarda kullanıldığını merak ediyorum. Üçgenin açılımı ile ilgili pratik uygulamalar ve örnekler de paylaşabilir misiniz?
Üçgen Çeşitleri ve Açıları
Üçgenler, kenar uzunluklarına ve açılarına göre farklı çeşitlere ayrılır. Üçgen çeşitleri arasında eşkenar, ikizkenar ve çeşitkenar üçgenler bulunur. Eşkenar üçgenin tüm kenar uzunlukları eşit olduğu için, iç açıları da 60°'dir. İkizkenar üçgende ise iki kenar eşit olup, buna bağlı olarak iki iç açısı da eşittir. Çeşitkenar üçgende ise tüm kenar ve açılar farklıdır.
Açıların Üçgen Üzerindeki Etkisi
Üçgenlerin açıları, geometrik şeklin özelliklerini ve kullanım alanlarını belirler. Örneğin, dik üçgenler, trigonometri ve mühendislik hesaplamalarında sıkça kullanılırken, eşkenar üçgenler simetri ve estetik tasarımlarda tercih edilmektedir. İkizkenar üçgenler ise bazı yapıların stabilitesinde önemli rol oynar.
Pratik Uygulamalar ve Örnekler
Gündelik hayatta üçgenlerin kullanım alanları oldukça fazladır. Örneğin, bir çatının üçgen şeklinde tasarlanması, suyun akışını kolaylaştırır ve yapının dayanıklılığını artırır. Ayrıca, üçgenler inşaat mühendisliğinde yük dağılımını optimize etmek için kullanılır. Trigonometri ile ilgili hesaplamalar yapmak için dik üçgenlerden yararlanarak, yükseklik ölçümü veya uzaklık hesaplama gibi pratik uygulamalar gerçekleştirilebilir.
Bu bilgiler ışığında, üçgenlerin hem teorik hem de pratik açıdan ne kadar önemli olduğunu görebiliriz. Her bir üçgen türü, farklı durumlar ve hesaplamalar için avantajlar sunar.
Üçgenin açılımı konusundaki bilgiler oldukça faydalı. Özellikle üçgenlerin çeşitleri ve özellikleri çok önemli. Üçgenin açılımını anlamak, geometri ve trigonometri derslerinde büyük kolaylık sağlıyor. Üçgenlerin alan hesaplamaları da pratikte sıkça karşılaşılan bir durum. Bu konuda daha fazla örnek görmek ilginç olurdu.
Sevil,
Üçgenin Önemi
Üçgenler, geometri ve trigonometri derslerinde temel yapı taşlarıdır. Üçgenlerin çeşitleri ve özellikleri, matematiksel kavramların daha iyi anlaşılmasına yardımcı olur. Özellikle üçgenlerin açıları ve kenarları arasındaki ilişki, birçok matematiksel problemde kritik bir rol oynar.
Alan Hesaplamaları
Ayrıca, üçgenlerin alan hesaplamaları günlük hayatta da sıkça kullanılır. Bu hesaplamalar, mimariden mühendisliğe kadar birçok alanda önemli bir yere sahiptir. Farklı üçgen türlerine göre alan hesaplama yöntemleri de değişiklik gösterir.
Daha Fazla Örnek İsteği
Daha fazla örnek görmek istemen, konuyu daha iyi kavrayabilmen açısından oldukça faydalı olacaktır. Farklı üçgen türleri ve çeşitli alan hesaplama yöntemleri üzerine örnekler, bu bilgileri pekiştirmene yardımcı olabilir. Eğer belirli bir konu veya örnek ile ilgili bir isteğin varsa, onu da paylaşabilirsin.
Üçgenin açıları ve elemanları arasındaki ilişkiler oldukça önemli. Üçgenin açılımları, özellikle tepe ve taban açıları arasındaki bağlantılar, geometri öğreniminde temel bir yer tutuyor. Üçgen çeşitleri de açıların farklı kombinasyonları ile belirleniyor. Peki, üçgenin açılarını anlamada en etkili yöntemler neler?
Üçgenin Açıları ve Elemanları
Polatkan, üçgenin açıları ve elemanları arasındaki ilişkileri anlamak için birkaç temel yöntemi göz önünde bulundurmak önemlidir. Öncelikle, üçgenin iç açılarının toplamının 180 derece olduğunu bilmek, açıların birbirleriyle olan ilişkilerini kavramada önemli bir adımdır. Bu temel bilgi, üçgenin farklı türlerini (eşkenar, ikizkenar, çarpık) tanımlarken de rehberlik eder.
Çizim ve Görselleştirme
Üçgenin açılarını anlamanın en etkili yollarından biri, çizim yapmaktır. Üçgen çizerek açıları etiketlemek ve ölçmek, soyut kavramları somut hale getirir. Ayrıca, açıları farklı renklerle göstererek, tepe ve taban açıları arasındaki ilişkileri daha net bir şekilde görselleştirebilirsiniz.
Formüller ve Teoremler
Teoremler ve formüller de bu ilişkileri anlamada büyük yardımcıdır. Örneğin, "İkizkenar Üçgen Teoremi" ya da "Dış Açı Teoremi" gibi temel teoremleri öğrenmek, açıların birbirleriyle olan ilişkilerini daha iyi kavramanızı sağlar.
Pratik Problemler
Aynı zamanda, pratik problemler üzerinde çalışmak da açıların ilişkilerini anlamaya yardımcı olur. Farklı üçgen türlerinde açıları hesaplama ve bulma alıştırmaları yapmak, teorik bilgiyi pratiğe dökerek pekiştirir.
Sonuç olarak, Polatkan, üçgenin açıları ve elemanları arasındaki ilişkileri anlamada çizim yapma, teoremleri öğrenme ve pratik problemler çözme gibi yöntemleri kullanmak oldukça etkili olacaktır. Bu yöntemler, geometri konusundaki bilgi ve anlayışınızı derinleştirecektir.
Üçgenin açılımı ile ilgili olarak, bu konuda daha fazla bilgi edinmek için hangi kaynakları önerirsiniz? Üçgenlerin çeşitleri ve özellikleri üzerine detaylı bir çalışma yapmanın yanı sıra, piramit açılımı gibi diğer geometrik şekillerin açılımlarını da öğrenmek istiyorum. Bu konuda ne yapmalıyım?
Kaynak Önerileri
Üçgenin açılımı ve geometrik şekiller hakkında daha fazla bilgi edinmek için çeşitli kaynaklar mevcuttur. İlk olarak, matematik ders kitapları ve geometri kitapları, üçgenler ve diğer geometrik şekillerin özellikleri hakkında detaylı bilgiler sunar. Özellikle “Geometri” başlıklı kitaplar, üçgenlerin çeşitleri ve özellikleri gibi konuları kapsamlı bir şekilde ele alır.
Online Kaynaklar
YouTube gibi video paylaşım platformlarında, geometri dersleri ve açılımlarını anlatan eğitim videoları bulabilirsiniz. Ayrıca Khan Academy, Coursera veya Udemy gibi online eğitim platformlarında geometri ile ilgili kurslar alarak konuyu derinlemesine inceleyebilirsiniz.
Pratik Çalışmalar
Üçgenler ve diğer geometrik şekiller üzerinde pratik yapmak, konuyu daha iyi anlamanıza yardımcı olacaktır. Geometrik şekilleri çeşitli yazılımlar (GeoGebra gibi) kullanarak modelleyebilir veya kağıt üzerinde şemalar çizebilirsiniz.
Üçgenlerin Çeşitleri
Üçgenler, eşkenar, ikizkenar ve çeşitkenar olarak sınıflandırılır. Bu üçgenlerin özelliklerini öğrenmek, açılımlarını anlamak için önemlidir. Her bir üçgen türünün açılımına dair çizimler yaparak pekiştirebilirsiniz.
Piramit Açılımı
Piramit açılımı için de benzer kaynaklardan faydalanabilirsiniz. Piramitlerin açılımı genellikle üçgenler ile ilgilidir, bu nedenle üçgenler hakkındaki bilgilere de başvurmak iyi bir başlangıç olacaktır.
Bu bilgileri göz önünde bulundurarak, sistematik bir çalışma yapabilir ve geometrik şekillerin açılımlarını daha iyi öğrenebilirsiniz. Başarılar dilerim!
Üçgen piramit açılımı hakkında bilgi verir misiniz? Üçgen piramitin yüzey alanını hesaplamak için hangi formülleri kullanmalıyız? Ayrıca, üçgen piramidin açılımını görsel olarak nasıl ifade edebiliriz? Bu konuda biraz daha detay verirseniz çok sevinirim.
Üçgen Piramit Nedir?
Üçgen piramit, tabanı üçgen olan ve üçgen tabanın köşelerinden birinin üst noktasına doğru yükselen üçgen yüzeylere sahip bir üç boyutlu geometrik şekildir. Genellikle "tetrahedron" olarak da adlandırılır.
Yüzey Alanı Hesaplama Formülleri
Üçgen piramidin yüzey alanını hesaplamak için genellikle şu formüller kullanılır:
1. Taban Alanı: Taban üçgeninin alanını hesaplamak için, üçgenin taban uzunluğu (a) ve yüksekliği (h) kullanılarak:
\[ \text{Taban Alanı} = \frac{1}{2} \times a \times h \]
2. Yan Yüzey Alanı: Her bir yan yüz, üçgen şeklindedir. Yan yüzeylerin toplam alanı için her bir yüzey alanını ayrı ayrı hesaplayıp toplamak gerekmektedir. Eğer yan yüzlerin yüksekliği (l) ve taban uzunluğu (a) biliniyorsa:
\[ \text{Yan Yüzey Alanı} = \frac{1}{2} \times a \times l \]
Üçgen piramidin toplam yüzey alanı:
\[ \text{Toplam Yüzey Alanı} = \text{Taban Alanı} + 3 \times \text{Yan Yüzey Alanı} \]
Açılımın Görsel İfadesi
Üçgen piramidin açılımını görsel olarak ifade etmek için, piramidin tabanını düz bir yüzeyde çizebiliriz. Daha sonra, her bir yan yüzün açılımını tabanın kenarları boyunca çizebiliriz. Yan yüzler üçgen şeklinde olup, tabanın her bir kenarına yaslanır. Böylece, açılımda bir üçgen ve üç tane yan üçgen yer alır. Bu açılım, üçgen piramidin şeklinin daha iyi anlaşılmasını sağlar.
Umarım bu bilgiler yardımcı olur!
Geometri dersinde üçgenlerin tanımını öğrenmek oldukça önemli. Üçgenin tanımı nedir diye sorduğumuzda, üç kenarı ve üç köşesi olan bir şekil olarak tanımlanıyor. Ayrıca, üçgenin iç açıları toplamı 180 derece olduğundan bahsetmek de gerekiyor. Bu bilgiler, üçgenlerin özelliklerini daha iyi anlamak için temel bir başlangıç oluşturuyor. Üçgenler, kenar uzunluklarına ve açılarına göre çeşitli türlere ayrılıyor ve bu çeşitlilik, geometri çalışmalarını daha ilginç hale getiriyor. Üçgenin tanımı nedir sorusu, geometri eğitiminde sıkça karşımıza çıkan bir soru ve bu konuya hakim olmak, matematiksel düşünme becerimizi geliştirmemize yardımcı oluyor.
Üçgenin Tanımı
Artimur, üçgenler geometri dersinde temel bir kavramdır ve doğru bir tanımına sahip olmak oldukça önemlidir. Üçgen, üç kenarı ve üç köşesi olan bir çokgendir. Bu basit tanım, daha karmaşık geometrik yapıların anlaşılmasında da temel bir rol oynar.
İç Açıların Toplamı
Üçgenin iç açıları toplamının 180 derece olduğu bilgisi, geometri dersinde sıkça vurgulanan bir noktadır. Bu özellik, üçgenlerin çeşitli türlerini anlamamıza ve farklı açılarla ilgili problemleri çözmemize yardımcı olur.
Üçgenlerin Çeşitleri
Üçgenler, kenar uzunluklarına ve açılarına göre eşit kenar, ikizkenar ve çeşitkenar gibi farklı türlere ayrılır. Bu çeşitlilik, geometrik çalışmaların derinliğini artırır ve konunun anlaşılmasını kolaylaştırır.
Matematiksel Düşünme Becerileri
Sonuç olarak, üçgenin tanımını bilmek ve bu konudaki temel bilgileri öğrenmek, matematiksel düşünme becerimizi geliştirmek için oldukça faydalıdır. Geometri alanında sağlam bir temel oluşturarak daha ileri konulara geçiş yapmamızı sağlar.
Ãçgen çeşitleri arasında ikizkenar üçgenlerin taban açılarının birbirine eşit olduğunu belirtmişsiniz. Peki, bu durumda ikizkenar üçgenin tepe açısının özellikleri nelerdir ve bu özellikler üzerinde nasıl hesaplamalar yapılabilir?
Merhaba Rikab,
İkizkenar üçgenlerin özelliklerinden biri olan taban açılarının eşit olması, tepe açısının özelliklerini ve hesaplamalarını da etkiler. İkizkenar üçgenin tepe açısı, taban açılarının toplamının 180°'den çıkarılmasıyla bulunur. İşte bu hesaplamalar ve özellikler hakkında daha detaylı bilgiler:
Tepe Açısının Hesaplanması:
- İkizkenar üçgenin iç açılarının toplamı her üçgende olduğu gibi 180°'dir.
- Taban açılarının her biri A olsun. O halde tepe açısı (T) şu şekilde hesaplanır: T = 180° - 2A
Özellikleri:
- Tepe açısının büyük veya küçük olması, taban açılarının büyüklüğüne bağlıdır. Taban açıları ne kadar büyükse, tepe açısı o kadar küçük olur ve tersi de geçerlidir.
- Eğer ikizkenar üçgenin taban açıları eşitse, tepe açısının da simetrik bir şekilde ortadan ikiye bölündüğünü söyleyebiliriz. Bu durumda tepe noktasından tabana çizilen dikme, üçgeni iki eşit dik üçgene böler.
Örnek Hesaplama:
- Diyelim ki bir ikizkenar üçgende taban açılarının her biri 40° olsun. O zaman tepe açısı şu şekilde hesaplanır: T = 180° - 240° = 100°
Bu özellikleri ve hesaplamaları kullanarak ikizkenar üçgenin tepe açısını ve diğer açılarla olan ilişkisini rahatlıkla belirleyebilirsiniz.
Sevgiler,
Assistant
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?