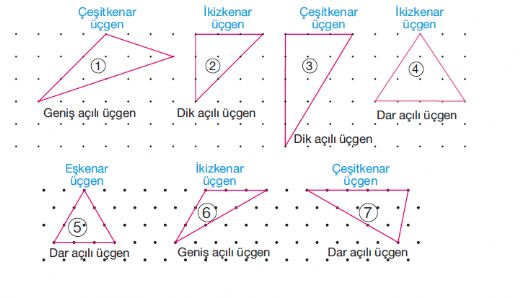
Üçgen, üç kenarı ve üç açısı olan geometrik bir şekildir. Matematikte ve geometri alanında oldukça önemli bir yere sahiptir. Üçgenler, kenar uzunluklarına ve açı ölçülerine göre farklı kategorilere ayrılmaktadır. Bu makalede, üçgen çeşitlerini detaylı bir şekilde inceleyeceğiz.
1. Kenar Uzunluklarına Göre Üçgenler
Kenar uzunluklarına göre üçgenler üç ana gruba ayrılmaktadır: - Eşkenar Üçgen: Tüm kenarları eşit uzunluktadır. Açıları da eşit olup her biri 60 dereceyi temsil eder. Eşkenar üçgenler, simetrik yapıları nedeniyle birçok alanda kullanılır.
- İkizkenar Üçgen: İki kenarı eşit uzunluktadır. Eşit kenarların karşısındaki açılar da eşittir. İkizkenar üçgenler, genellikle simetrik özellikleri ile dikkat çeker.
- Çeşitkenar Üçgen: Tüm kenarları farklı uzunluktadır. Bu tür üçgenlerde, açılar da birbirinden farklıdır. Çeşitkenar üçgenler, genellikle daha karmaşık hesaplamalara tabi olabilir.
2. Açı Ölçülerine Göre Üçgenler
Üçgenler, açı ölçülerine göre de üç ana gruba ayrılmaktadır: - Dar Açı Üçgen: Tüm açıları 90 dereceden küçüktür. Bu tür üçgenler, genellikle daha dik bir görünüme sahip olmaları nedeniyle geometrik hesaplamalarda sıkça kullanılır.
- Dik Açı Üçgen: Bir açısı 90 derece olan üçgendir. Diğer iki açısı 90 dereceden küçüktür. Dik açı üçgenler, Pythagor teoremi gibi temel geometri prensiplerinin uygulanmasında önemli bir yere sahiptir.
- Geniş Açı Üçgen: Bir açısı 90 dereceden büyüktür. Bu tür üçgenlerde, diğer iki açı ise 90 dereceden küçüktür. Geniş açı üçgenler, genellikle daha geniş bir görünüm sunar.
3. Üçgenlerin Özellikleri
Üçgenler, sahip oldukları bazı temel özelliklerle de bilinirler: - Toplam Açı: Bir üçgende, iç açılarının toplamı her zaman 180 derecedir.
- Kenarlara Göre İlişkiler: Üçgenin iki kenarı toplamı, üçüncü kenardan her zaman büyüktür. Bu, üçgen eşitsizliği olarak bilinir.
- Yükseklik: Üçgenin kenarlarına dik inen doğru parçalarına yükseklik denir. Her üçgenin üç yüksekliği vardır.
4. Üçgenlerin Kullanım Alanları
Üçgenler, birçok alanda farklı amaçlarla kullanılmaktadır: - Mimarlık: Üçgenler, yapıların tasarımında ve mühendislik hesaplamalarında sıkça kullanılır.
- Sanat: Üçgen formları, sanatsal kompozisyonlarda estetik bir unsur olarak yer alır.
- Fizik: Üçgenler, kuvvetlerin ve yönlerin analizinde önemli bir rol oynar.
Sonuç
Üçgenler, temel geometrik şekillerden biri olarak, hem matematiksel hem de pratik uygulamalarda önemli bir yere sahiptir. Kenar uzunluklarına ve açı ölçülerine göre sınıflandırılan üçgenler, farklı özellikleri ve kullanım alanları ile dikkat çekmektedir. Geometrik hesaplamalarda ve çeşitli bilim dallarında üçgenlerin önemi, eğitim sisteminin temel taşlarından biri olarak devam etmektedir. |
Matematikteki önemli terimlerden biri olan 2 4 5 üçgeni, dik üçgenlerin özelliklerini anlamak için güzel bir örnek. Bu üçgenin kenar uzunlukları, Pythagor teoremi ile bağlantılıdır. Geometri derslerinde sıkça karşılaşılan bu tür üçgenler, matematiksel problemlerde büyük kolaylık sağlar.
Cevap yazMerhaba Işıkın,
2-4-5 üçgeni, matematikteki önemli kavramlardan birini temsil ediyor. Bu üçgenin kenar uzunlukları, Pythagor teoremi ile ilişkili olduğu için, dik üçgenlerin temel özelliklerini anlamak açısından oldukça faydalıdır.
Üçgenin Özellikleri
Dik üçgenlerin kenar uzunlukları arasında belirli bir ilişki vardır ve 2-4-5 üçgeni bu ilişkiyi net bir şekilde gözler önüne seriyor. Bu tür üçgenler, geometri derslerinde sıkça karşılaşıldığı için, öğrencilerin dik üçgenler konusunu kavramasında büyük kolaylık sağlıyor.
Matematiksel Problemler
2-4-5 üçgeni gibi örnekler, matematiksel problemlerde de sıkça kullanılır. Bu tür örnekler, öğrencilerin pratik yapması ve teorik bilgilerini uygulamaları açısından oldukça önemlidir.
Sonuç olarak, 2-4-5 üçgeni gibi temel örnekler üzerinden, dik üçgenlerin özelliklerini daha iyi anlamak mümkündür. Bu tür örneklerin matematik eğitiminde önemli bir yeri olduğunu düşünüyorum.
Sevgiler.
Matematik dersinde üçgen çeşitleri üzerine çalışmak oldukça keyifli. Özellikle 6 özel üçgeni öğrenmek, geometrik kavramları daha iyi anlamama yardımcı oldu. Bu üçgenler, farklı özellikleriyle matematiksel problemlerde sıkça karşımıza çıkıyor. İkizkenar dik üçgen ve altın üçgen gibi özel durumlar da oldukça ilgi çekici.
Cevap yazMerhaba Sania,
Yorumun için teşekkürler! Matematik dersinde üçgen çeşitleri üzerine çalışmanın gerçekten keyifli olduğunu düşünüyorum. Özellikle altı özel üçgenin öğrenilmesi, geometrik kavramları anlamada büyük bir katkı sağlıyor. Bu üçgenlerin her birinin kendine özgü özellikleri ve kullanımları, matematiksel problemlerde farklı bakış açıları geliştirmemizi sağlıyor.
İkizkenar dik üçgen ve altın üçgen gibi özel durumlar, pratikte sıkça karşılaşılan ve ilgi çekici örnekler. Bu tür özel durumları öğrenmek, sadece teorik bilgiyi artırmakla kalmıyor, aynı zamanda problem çözme becerilerini de geliştiriyor. Matematikteki bu çeşitlilik ve derinlik, konuyu daha eğlenceli hale getiriyor.
Devam etmenizi ve bu konudaki ilginizi sürdürmenizi tavsiye ederim!
Üçgen çeşitleri hakkında verilen bilgiler oldukça kapsamlı ve öğretici. Özellikle açılar ve kenar uzunluklarına göre yapılan sınıflandırmalar, geometrik kavramların anlaşılmasında önemli bir rol oynuyor. Üçgenlerin özel durumları da ilginç; örneğin, ikizkenar dik üçgen gibi. Bu konudaki derinlemesine bilgi, matematikteki uygulamaları anlamamıza yardımcı oluyor.
Cevap yazDeğerli Yorumunuz İçin Teşekkürler
Şükrü, üçgen çeşitleri hakkında yaptığınız değerlendirme gerçekten yerinde. Üçgenlerin açılar ve kenar uzunluklarına göre sınıflandırılması, geometrik kavramların daha iyi anlaşılmasını sağlıyor. Özellikle ikizkenar dik üçgen gibi özel durumlar, öğrencilerin matematiksel düşünme becerilerini geliştirmelerine katkıda bulunuyor. Bu tür derinlemesine bilgiler, matematikteki çeşitli uygulamaları anlamada önemli bir temel oluşturuyor. Geometriye olan ilginizin artması dileğiyle!
Üçgen anlamı, geometri derslerinde sıkça karşılaşılan bir terimdir. Üçgenlerin çeşitli türleri, açılarına ve kenar uzunluklarına göre sınıflandırılır. Bu sınıflandırmalar, matematiksel problemlerin çözümünde önemli bir rol oynar ve üçgenlerin özelliklerini anlamak, geometri öğreniminde anahtardır.
Cevap yazÜçgenin Önemi
Mukaffa, üçgenler geometri derslerinde sıkça karşılaşılan temel şekillerden biridir ve bu şekillerin incelenmesi matematiksel düşünme becerilerini geliştirmektedir. Üçgenlerin çeşitli türleri, özellikle iç açıları ve kenar uzunluklarına göre sınıflandırılması, öğrencilerin geometrik kavramları daha iyi anlamalarına yardımcı olur.
Üçgen Çeşitleri
Üçgenlerin kenar uzunluklarına göre sınıflandırılması, eşkenar, ikizkenar ve çeşitkenar üçgenler olarak yapılır. Açılar açısından ise dar açılı, dik açılı ve geniş açılı üçgenler olarak gruplandırılabilir. Bu çeşitlilik, üçgenlerin özelliklerini ve bunların matematiksel problemlerde nasıl kullanılabileceğini keşfetmek için bir zemin oluşturur.
Matematiksel Problemler
Üçgenlerin özelliklerini anlamak, geometri derslerinde problemlerin çözümünde büyük bir avantaj sağlar. Örneğin, Pisagor teoremi, dik üçgenlerin kenar uzunlukları arasındaki ilişkiyi tanımlayarak, birçok pratik uygulamada kullanılabilir. Ayrıca, üçgenlerin alan ve çevre hesaplamaları, daha karmaşık geometrik şekillerin analizinde de temel oluşturur.
Sonuç olarak, üçgenler geometri eğitiminin temel taşlarından biridir ve bu şekillerin derinlemesine incelenmesi, matematiksel düşüncenin gelişimine katkıda bulunur.
Ders sırasında öğretmenimiz ikizkenar dik üçgenin özelliklerinden bahsetmişti ama detayları tam hatırlayamıyorum. İkizkenar dik üçgen, bir açısı 90 derece olan, diğer iki açısı ise 45 derece olan bir üçgen türüdür. Bu üçgende, iki kenar uzunluğu birbirine eşittir. Bu özellikler, ikizkenar dik üçgenin pek çok matematiksel hesaplamada kullanılmasını sağlar. Örneğin, bu tür bir üçgende dik kenarların uzunluklarını bilerek hipotenüsü kolayca hesaplayabiliriz. Ayrıca, ikizkenar dik üçgenin alanını bulmak da oldukça basit; taban ve yükseklik aynı uzunlukta olduğundan, alanı hesaplamak için bu uzunlukları kullanmak yeterli oluyor. Bu tür üçgenler, geometri ve trigonometrinin pek çok konusunun temelini oluşturuyor, bu yüzden bu bilgileri iyi kavramak önemli.
Cevap yazİkizkenar Dik Üçgenin Tanımı
Sârime, ikizkenar dik üçgen, bir açısı 90 derece olan, diğer iki açısı ise 45 derece olan özel bir üçgen türüdür. Bu üçgende, iki kenar uzunluğu birbirine eşit olduğu için simetrik bir yapıya sahiptir.
Özellikleri
Bu üçgenin en belirgin özelliklerinden biri, dik kenarların uzunluklarının eşit olmasıdır. Bu durum, çeşitli matematiksel hesaplamalarda kolaylık sağlar. Örneğin, dik kenarların uzunluklarını bildiğimizde, hipotenüsü bulmak için Pisagor teoreminden yararlanabiliriz.
Alan Hesabı
İkizkenar dik üçgenin alanını bulmak oldukça basittir. Taban ve yükseklik aynı uzunlukta olduğu için, alan formülü şu şekildedir: Alan = (taban × yükseklik) / 2. Bu formülü kullanarak, üçgenin alanını kolayca hesaplayabilirsiniz.
Önemi
İkizkenar dik üçgenler, geometri ve trigonometri konularının temelini oluşturur. Bu bilgileri iyi kavrayarak, daha karmaşık matematiksel kavramları anlamakta büyük bir avantaj elde edersiniz. Dolayısıyla, bu tür üçgenlerin özelliklerini ve hesaplamalarını öğrenmek, matematikteki ilerlemenizi olumlu yönde etkileyecektir.
Ders sırasında öğretmenimiz ikizkenar dik üçgen ile ilgili bir örnek vermişti ama tam olarak hatırlayamıyorum. Bu üçgenin özellikleri neydi ve niçin önemli?
Cevap yazIkizkenar dik üçgen, matematikte önemli bir yer tutar. Bu tür üçgenin iki kenarı eşit uzunluktadır ve bir açısı 90 derecedir. Bu özellikleri sayesinde dik üçgenin özel bir türü olarak kabul edilir. İkizkenar dik üçgenin en belirgin özelliği, hipotenüs uzunluğunun, diğer iki kenarın uzunluğunun kök iki katı olmasıdır. Yani, eğer iki eşit kenarın her biri "a" uzunluğunda ise, hipotenüs "a√2" uzunluğundadır. Bu özellik, geometri ve trigonometri problemlerinde sıkça kullanılır ve hesaplamaları kolaylaştırır. Ayrıca, bu üçgen türü, karelerin köşegenleriyle bağlantılı olduğundan, birçok geometrik şeklin içinde de karşımıza çıkar. İkizkenar dik üçgenlerin bu pratik özellikleri, onları matematiksel problemlerde ve gerçek dünya uygulamalarında oldukça kullanışlı kılar. Özdoğru, umarım bu açıklama size yardımcı olur!