Üçgen Alan Formülü Nelerdir?

Üçgenler, geometri alanında önemli bir yere sahip temel şekillerdir. Alanlarının hesaplanması için farklı yöntemler mevcuttur. Bu içerikte, üçgen alanını hesaplamak için kullanılan formüller ve yöntemler detaylı bir şekilde incelenecektir.

Konu kakkında 1 soru soruldu ve cevaplandı

Üçgen Alan Formülü Nedir?

Üçgen, temel geometrik şekillerden biri olup, üç kenarı ve üç açısı bulunan birçokgendir. Üçgenin alanını hesaplamak için çeşitli formüller kullanılmaktadır. Bu makalede, üçgen alanı hesaplama yöntemleri detaylı bir şekilde ele alınacaktır.

Üçgenin Temel Özellikleri

Üçgenlerin bazı temel özellikleri şunlardır:

Üçgen, üç kenarı ve üç açısı olan birçokgendir.
Üçgenin iç açılarının toplamı 180 dereceye eşittir.
Üçgenin kenar uzunlukları, alan hesaplamalarında kritik bir rol oynar.

Üçgen Alan Formülü

Bir üçgenin alanını hesaplamak için en yaygın kullanılan formül:\[ \text{Alan} = \frac{1}{2} \times \text{Taban} \times \text{Yükseklik} \]Bu formülde, taban üçgenin herhangi bir kenarıdır ve yükseklik, bu kenara dik olarak çizilen doğru parçasıdır.

Üçgen Alanını Hesaplamak İçin Diğer Yöntemler

Üçgen alanını hesaplamak için birkaç farklı yöntem bulunmaktadır. Bunlar:

Heron Formülü: Üç kenar uzunluğu \(a\), \(b\) ve \(c\) olan bir üçgenin alanı, Heron formülü ile de hesaplanabilir:\[ s = \frac{a + b + c}{2} \]\[ \text{Alan} = \sqrt{s(s-a) (s-b) (s-c)} \]Burada \(s\) üçgenin yarı çevresidir.
Trigonometri Kullanarak Alan Hesaplama: Eğer bir üçgenin iki kenar uzunluğu ve aralarındaki açı biliniyorsa, alan şu şekilde hesaplanabilir:\[ \text{Alan} = \frac{1}{2} \times a \times b \times \sin(C) \]Burada \(a\) ve \(b\) kenar uzunlukları, \(C\) ise bu iki kenarın arasındaki açıdır.
Koordinat Düzleminde Üçgen Alanı Hesaplama: Üçgenin köşe noktaları \((x_1, y_1)\), \((x_2, y_2)\) ve \((x_3, y_3)\) olarak verildiğinde, alan hesaplama formülü şu şekildedir:\[ \text{Alan} = \frac{1}{2} | x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) | \]

Üçgen Alanı Hesaplamada Dikkat Edilmesi Gerekenler

Üçgen alanı hesaplanırken aşağıdaki hususlara dikkat edilmelidir:

Tabanın ve yüksekliğin doğru bir şekilde belirlenmesi, alan hesaplamasının doğruluğu için esastır.
Heron formülünde kenar uzunluklarının doğru bir şekilde ölçülmesi gerekmektedir.
Trigonometrik hesaplamalarda açıların doğru birimlerde (derece veya radian) kullanılması önemlidir.

Sonuç

Üçgen alanı hesaplama, temel geometrik bilgilerle gerçekleştirilebilen bir işlemdir. Farklı yöntemlerin bilinmesi, çeşitli üçgen türleri için doğru alan hesaplamalarını yapma imkanı sunar. Bu bilgiler, matematiksel problemlerin çözümünde ve mühendislik uygulamalarında oldukça faydalıdır.

Yeni Soru Sor / Yorum Yap

Sizden Gelen Sorular / Yorumlar

Torlak 12 Temmuz 2024 Cuma

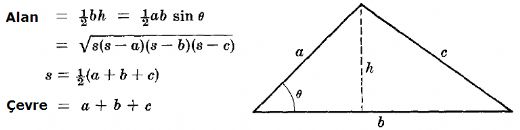
Bu üçgen alan formüllerini kullanarak farklı üçgen türlerinin alanlarını hesaplamak gerçekten işe yarıyor mu? Özellikle bir açısı ve bu açısının kenarları bilinen üçgenler için hangi durumlardan faydalanabiliriz?

Admin 12 Temmuz 2024 Cuma

Merhaba Torlak,

Evet, üçgen alan formüllerini kullanarak farklı üçgen türlerinin alanlarını hesaplamak oldukça işe yarar. Özellikle bir açısı ve bu açının kenarları bilinen üçgenler için Sinüs Teoremi'nden faydalanabilirsiniz. Bu teoreme göre, bir üçgenin alanı şu formülle hesaplanabilir:

Alan = 1/2 a b sin(C)

Burada, a ve b açının kenarları, C ise bu kenarın açısıdır. Bu formül, özellikle iki kenarı ve aralarındaki açıyı bildiğiniz üçgenler için çok kullanışlıdır. Ayrıca, Heron formülü de kenar uzunlukları bilinen üçgenlerin alanını hesaplamak için kullanılabilir. Bu çeşit hesaplamalar geometri problemlerinde sıklıkla işinizi kolaylaştırır.