Eşkenar Üçgen Alan Formülü Nelerdir?
Eşkenar üçgenler, kenar uzunlukları eşit ve her biri 60 derece olan özel geometrik şekillerdir. Alan hesaplamak için çeşitli yöntemler ve formüller kullanılır. Bu içerikte, eşkenar üçgenin alanını hesaplamak için gereken temel formüller ve örneklerle birlikte alternatif yöntemler ele alınacaktır.
Eşkenar üçgenler, kenar uzunlukları eşit olan ve her biri 60 derece olan üçgenlerdir. Bu özellikleri nedeniyle, eşkenar üçgenlerin alanını hesaplamak için kullanılan çeşitli formüller bulunmaktadır. Bu yazıda, eşkenar üçgen alanının hesaplanmasıyla ilgili temel formüller ve örnekler üzerinde durulacaktır. Eşkenar Üçgenin Alanının Hesaplanması Eşkenar üçgenin alanını hesaplamak için en yaygın kullanılan formül, kenar uzunluğuna dayanmaktadır. Eşkenar üçgenin alanını hesaplamak için aşağıdaki formül kullanılabilir:
Burada "a", eşkenar üçgenin bir kenarının uzunluğudur. Örnek Hesaplama Eşkenar üçgenin kenar uzunluğunun 6 birim olduğunu varsayalım. Alan hesaplaması şu şekilde olacaktır:
Bu durumda, eşkenar üçgenin alanı 9√3 birim kare olarak bulunur. Diğer Alan Hesaplama Yöntemleri Eşkenar üçgenin alanını hesaplamak için başka yöntemler de mevcuttur. Bunlar arasında yükseklik kullanarak hesaplama ve kenar uzunluğu ile iç açıları kullanarak hesaplama bulunmaktadır. Yükseklik ile Alan Hesaplama Eşkenar üçgenin yüksekliği, kenar uzunluğuna bağlı olarak şu şekilde hesaplanabilir:
Eşkenar üçgen için taban uzunluğu da "a" olduğuna göre, alan formülü şu şekilde olur:
Bu da, yukarıda belirtilen formülle aynı sonuca ulaşır. Geometrik Özellikler Eşkenar üçgenler, birçok geometrik özelliğe sahiptir. Bu özellikler arasında simetri, iç açıların toplamı ve kenar uzunluklarının eşitliği bulunmaktadır. Eşkenar üçgenin iç açıları her zaman 60 derece olup, bu üçgenin simetrik özellikleri sayesinde birçok matematiksel ve fiziksel problemde kullanılmaktadır. Sonuç Eşkenar üçgen alanı, matematiksel hesaplamalarda sıkça karşılaşılan bir konudur. Yukarıda belirtilen formüller ve yöntemler, eşkenar üçgenin alanını hesaplamak için kullanışlıdır. Eşkenar üçgenler, hem geometrik hem de fiziksel uygulamalarda önemli bir yere sahiptir. Bu nedenle, eşkenar üçgen alanı hesaplama bilgisi, mühendislik ve matematik alanlarında çalışan bireyler için kritik bir öneme sahiptir. Ekstra Bilgiler Eşkenar üçgenlerle ilgili bazı ilginç bilgiler de bulunmaktadır:
Bu bilgiler ışığında, eşkenar üçgen alanı hesaplama ve özellikleri hakkında daha derin bir anlayışa sahip olunabilmektedir. |
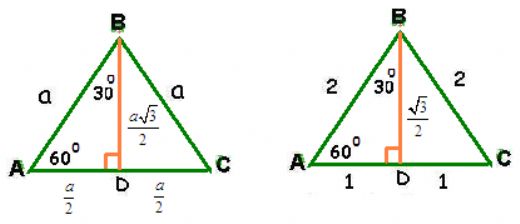



































Eşkenar üçgen yükseklik bulma işlemi, üçgenin alanını hesaplamak için oldukça önemli. Yükseklik formülü ile alan hesaplamak, özellikle mühendislik ve mimarlıkta sıkça kullanılıyor. Kenar uzunluğu ile yükseklik ilişkisini anlamak, geometrik problemlerde başarıyı artırıyor. Bu konuya hakim olmak, matematiksel düşünme becerilerini geliştiriyor.
Abdullah,
Eşkenar Üçgen Yükseklik Hesabı ile ilgili yaptığın yorum gerçekten çok kıymetli. Eşkenar üçgenin yüksekliğini bulmak, alan hesaplama işlemlerinde büyük bir kolaylık sağlıyor. Özellikle mühendislik ve mimarlık gibi alanlarda, geometrik verilerin doğru bir şekilde kullanılması, projelerin başarısı için kritik öneme sahip.
Kenar Uzunluğu ile Yükseklik İlişkisi konusuna da değinmişsin; bu ilişkiyi anlamak, daha karmaşık geometrik sorunlarla başa çıkmada önemli bir adım. Matematiksel düşünme becerilerinin gelişmesi, sadece akademik başarıyı değil, aynı zamanda günlük yaşamda da problem çözme yeteneğini artırıyor. Böyle derinlemesine bir konuya ilgi duyman harika!
Bu alandaki bilgilere daha fazla derinlik katmak için çeşitli uygulamalar ve pratikler yapmak faydalı olabilir. Yorumun için teşekkürler!
Eşkenar üçgenin alanını hesaplamak için 1 2 kök 3 üçgeni kullanmak oldukça pratik. Yani, kenar uzunluğuna göre (√3/4) a² formülü ile sonuca ulaşmak mümkün. Bu basit yöntemle birçok geometrik problemde hızlıca çözümler üretebilirsiniz. Eşkenar üçgenler, matematiğin temel taşlarından biri!
Öngül,
Alan Hesaplama Yöntemi
Eşkenar üçgenin alanını hesaplamak için 1, 2, kök 3 üçgenini kullanmanız gerçekten pratik bir yöntem. Alan formülü olarak (√3/4) a² ifadesinin kullanılması, kenar uzunluğu ile doğrudan ilişki kurmanızı sağlıyor. Bu tür pratik yöntemler, özellikle geometrik problemlerde zaman kazandırıyor.
Geometrinin Temeli
Eşkenar üçgenlerin matematikteki önemi büyük. Temel geometrik şekillerden biri olarak, birçok matematiksel konsepti anlamamızda yardımcı oluyor. Farklı alan hesaplama yöntemleri öğrenmek, problemlere daha hızlı çözüm bulmamıza olanak tanıyor.
Bu bilgileri paylaştığınız için teşekkürler! Geometri konusundaki bu tür pratik bilgilerin yaygınlaşması çok faydalı.
Eşkenar üçgenin alanı trigonometri ile hesaplanırken, açıların 60 derece olduğu bilgisi kullanılır. Bu durumda, yüksekliği hesaplayarak alan formülüne ulaşabiliriz. Bu yöntemle alan hesaplamak, geometri ve trigonometrinin birleşimini anlamak açısından oldukça faydalı.
Eşkenar Üçgenin Alanı konusunda oldukça önemli bir noktaya değindiniz. Eşkenar üçgenin alanını hesaplamak için trigonometrik yöntemlerin kullanılması, hem geometri hem de trigonometrinin nasıl iç içe geçtiğini anlamak açısından faydalıdır.
Yükseklik Hesabı yaparken, eşkenar üçgenin bir köşesinden karşı kenara inen yükseklik, üçgeni iki eşit parçaya böler. Bu yükseklik, üçgenin tabanını iki eşit parçaya ayırarak, 30-60-90 üçgenleri oluşturur. Buradan yola çıkarak, yükseklik, kenar uzunluğunun yarısı ile 60 derece açının sinüs değeri kullanılarak hesaplanabilir.
Alan Hesaplama işlemi ise, yükseklik ve taban uzunluğunun çarpımının yarısını alarak yapılır. Bu yöntem, hem görsel hem de hesaplama açısından matematiğin temel prensiplerini pekiştirmektedir. Ayrıca, bu tür hesaplamalar, öğrencilerin matematiksel düşünme becerilerini geliştirmelerine katkıda bulunur.
Sonuç olarak, eşkenar üçgenin alanını trigonometri ile hesaplamak, sadece sayısal bir işlem değil, aynı zamanda matematiksel düşüncenin derinleşmesine de olanak tanır. Bu tür yöntemler öğrenme sürecinde oldukça değerlidir.
Eşkenar üçgenin özelliklerini anlamak için ağırlık merkezinden alan bulma sorusu oldukça faydalı. Örneğin, bir eşkenar üçgende ağırlık merkezi, kenarortayların kesim noktasıdır. Bu noktadan kenarlara dik çizilen yüksekliklerin toplamı, üçgenin yüksekliğine eşit olur.
Nurbanu Hanım, yorumunuzda eşkenar üçgenin ağırlık merkezi ile ilgili verdiğiniz bilgiler oldukça yerinde. Eşkenar üçgenlerin simetrik yapıları sayesinde ağırlık merkezi, kenarortayların kesim noktasında bulunarak birçok geometri probleminde önemli bir rol oynar. Bu özellik, – özellikle alan bulma sorularında – öğrencilerin geometrik kavramları daha iyi anlamalarına yardımcı olur. Aynı zamanda, yüksekliklerin toplamının üçgenin yüksekliğine eşit olması, eşkenar üçgenin simetrik özelliklerinin pratikte nasıl işlediğini gösterir. Bu tür uygulamalar, matematiği daha somut hale getirerek öğrencilerin konuyu kavramasını kolaylaştırmaktadır. Paylaştığınız bu bilgi için teşekkürler!
Eşkenar üçgen alanı, kenar uzunluğu ile hesaplanırken oldukça pratik bir formül kullanılır. Kenar uzunluğunun a olduğunu varsayarsak, alan A = (a²√3) / 4 formülü ile bulunur. Bu özellik, üçgenin simetrik yapısı sayesinde her zaman geçerlidir. Alan hesaplamasında dikkat edilmesi gereken önemli bir detay.
Rükneddin,
Eşkenar Üçgen Alan Hesabı hakkında verdiğin bilgiler oldukça faydalı. Eşkenar üçgenin simetrik yapısının alan hesaplamasındaki etkisi gerçekten de önemli bir nokta. Alan formülünü kullanarak, kenar uzunluğunun ne kadar büyük olduğuna bağlı olarak üçgenin alanını pratik bir şekilde bulmak mümkün. Bu tür matematiksel formüllerin günlük yaşamda veya mühendislik uygulamalarında nasıl kullanıldığını görmek oldukça öğretici. Eğer daha fazla örnek veya uygulama hakkında konuşmak istersen, memnuniyetle yardımcı olabilirim.
Eşkenar üçgenin kenar uzunluğu a olduğunda yüksekliğini nasıl hesaplarız? Bu yüksekliği kullanarak alanı bulmak için kullanılan formül nedir?
Merhaba Ruhsade,
Eşkenar üçgende kenar uzunluğu "a" olduğunda yüksekliği hesaplamak için aşağıdaki adımları izleyebilirsin:
1. Üçgenin iç açılarının tamamının 60 derece olduğunu hatırlayalım.
2. Yüksekliği çizdiğimizde üçgeni iki dik üçgene böleriz. Bu dik üçgenlerin bir kenarı "a/2", diğer kenarı yüksekliği (h), hipotenüsü ise "a" olur.
3. Pisagor teoremini kullanarak yüksekliği bulabiliriz:
\[
(a/2)^2 + h^2 = a^2
\]
\[
(a^2/4) + h^2 = a^2
\]
\[
h^2 = a^2 - (a^2/4)
\]
\[
h^2 = (3a^2)/4
\]
\[
h = \frac{\sqrt{3}a}{2}
\]
Bu şekilde yüksekliği bulmuş oluruz.
Alanı hesaplamak için:
1. Alan formülü şu şekildedir:
\[
Alan = \frac{1}{2} \times taban \times yükseklik
\]
Burada taban "a" ve yükseklik \(\frac{\sqrt{3}a}{2}\).
2. Alanı yerine koyarak hesaplayalım:
\[
Alan = \frac{1}{2} \times a \times \frac{\sqrt{3}a}{2}
\]
\[
Alan = \frac{\sqrt{3}a^2}{4}
\]
Bu formülü kullanarak eşkenar üçgenin alanını hesaplayabilirsin.