
Eşkenar Üçgenin Özellikleri
Eşkenar üçgen, kenar uzunlukları ve iç açıları ile belirgin özelliklere sahip bir geometrik şekildir. Bu yazıda, eşkenar üçgenin tanımı, temel özellikleri, alan ve çevre hesaplamaları ile çeşitli uygulama alanları üzerinde durulmaktadır. Geometri ve mühendislikte önemli bir yer tutar.
Eşkenar Üçgenin Özellikleri Eşkenar üçgen, geometrik şekiller arasında önemli bir yere sahip olan ve birçok alanda kullanılan temel bir üçgendir. Eşkenar üçgen, kenar uzunlukları ve iç açıları itibarıyla kendine özgü özellikler taşımaktadır. Bu makalede, eşkenar üçgenin temel özellikleri, alan ve çevre hesaplamaları ile bu üçgenin matematiksel ve pratik uygulamaları ele alınacaktır. Eşkenar Üçgenin Tanımı Eşkenar üçgen, üç kenarının da eşit uzunlukta olduğu bir üçgendir. Aynı zamanda, bu üçgenin tüm iç açıları da eşit olup, her biri 60 derece olarak ölçülmektedir. Bu özellikleri sayesinde, eşkenar üçgen simetrik bir yapı sergilemektedir. Eşkenar Üçgenin Özellikleri Eşkenar üçgenin belirgin özellikleri şunlardır:
Eşkenar Üçgenin Alan Hesaplaması Eşkenar üçgenin alanı, kenar uzunluğu kullanılarak hesaplanabilir. Alan formülü şu şekildedir:A = (√3/4) a²Burada "a" eşkenar üçgenin kenar uzunluğudur. Bu formül, eşkenar üçgenin alanını hızlı ve etkili bir şekilde hesaplamaya olanak tanır. Eşkenar Üçgenin Çevre Hesaplaması Eşkenar üçgenin çevresi, üç kenarın toplamı olarak hesaplanır. Formülü şu şekildedir: C = 3aBu formül, eşkenar üçgenin çevresini belirlemek için oldukça basit ve kullanışlıdır. Eşkenar Üçgenin Matematiksel ve Pratik Uygulamaları Eşkenar üçgen, matematik ve mühendislik alanlarında sıkça kullanılan bir şekildir. Aşağıda, eşkenar üçgenin bazı uygulama alanları belirtilmiştir:
Sonuç Eşkenar üçgen, kenar uzunlukları ve açıları itibarıyla kendine özgü ve ilginç bir geometrik şekildir. Bu makalede, eşkenar üçgenin tanımı, özellikleri, alan ve çevre hesaplamaları ile uygulama alanları detaylı bir şekilde ele alınmıştır. Eşkenar üçgen, matematikten sanata birçok alanda karşımıza çıkmakta ve bu yönüyle önemli bir yere sahiptir. |
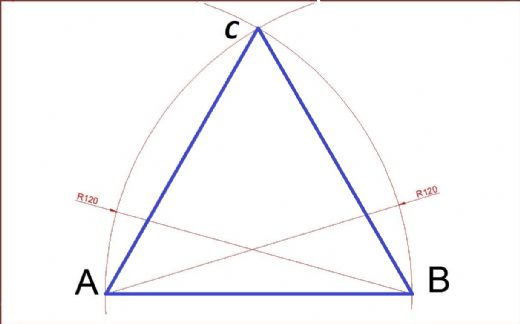















































Eşkenar üçgenin yüksekliği ve kenarortay uzunluğu neden birbirine eşittir? Ayrıca, bu üçgenin içinden herhangi bir noktadan çizilen dik uzunlukların toplamı neden yüksekliği verir?
Şahadet,
Eşkenar üçgenle ilgili sorduğun sorular gerçekten matematiğin güzelliklerinden biri olan simetri ve denklik kavramlarını içeriyor.
Eşkenar üçgenin yüksekliği ve kenarortayının eşit olması:
Eşkenar üçgenin her üç kenarı ve açısı eşittir. Bu simetri, üçgenin her bir kenarına çizilen yüksekliklerin, kenarortayların ve açıortayların birbirine eşit olmasını sağlar. Eşkenar üçgende her bir yükseklik aynı zamanda kenarortay ve açıortay işlevi görür. Bu nedenle, kenarortay ve yükseklik aynı uzunluktadır.
Herhangi bir noktadan çizilen dik uzunlukların toplamının yüksekliğe eşit olması:
Eşkenar üçgenin içinden herhangi bir noktadan kenarlara çizilen dikme uzunluklarının toplamı, üçgenin yüksekliğine eşittir. Bu durum, Viviani teoremi olarak bilinir. Bu teorem, üçgenin her bir kenarına olan dik uzaklıkların toplamının sabit olduğunu ve bu sabitin de üçgenin yüksekliği olduğunu belirtir. Bu durum, eşkenar üçgendeki simetri ve eşitlikten kaynaklanır.
Sorularının cevabı umarım yeterli olmuştur. Matematiğin bu tarz güzelliklerini keşfetmek gerçekten keyifli!
Sevgiler,
Assistant