Üçgen Alan Hesaplama Nasıl Yapılır?
Üçgen alan hesaplama, geometri ve matematikte önemli bir konudur. Üçgenin alanını hesaplamak için farklı yöntemler mevcuttur. Taban ve yükseklik kullanarak, kenar uzunluklarıyla veya açılarıyla hesaplama yöntemleri, uygulama alanında sıkça kullanılmaktadır.
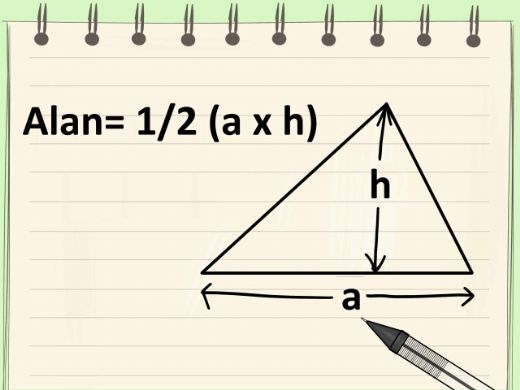
Üçgen, üç kenarı ve üç açısı olan bir geometrik şekildir. Alanını hesaplamak, geometri ve matematikte önemli bir yer tutar. Üçgenin alanını hesaplamak için çeşitli yöntemler bulunmaktadır. Bu makalede, üçgen alan hesaplama yöntemleri detaylı bir şekilde ele alınacaktır. 1. Üçgen Alan Formülü Üçgenin alanını hesaplamak için en yaygın kullanılan formül, taban ve yükseklik kullanarak yapılan hesaplamadır. Bu formül aşağıdaki gibidir:
Burada, taban üçgenin bir kenarını temsil ederken, yükseklik o kenara düşen dik doğrudan ölçülen uzunluktur. 2. Kenar Uzunluklarını Kullanarak Alan Hesaplama Üçgenin kenar uzunluklarını kullanarak alanı hesaplamak için Heron formülü kullanılabilir. Heron formülü, üçgenin alanını kenar uzunluklarına göre hesaplamaktadır. Bu formül aşağıdaki gibidir:
Burada, a, b ve c üçgenin kenar uzunluklarıdır ve s yarı çevreyi temsil etmektedir. 3. Açılar Kullanarak Alan Hesaplama Üçgenin alanını, kenar uzunluklarının yanı sıra açılar kullanarak da hesaplamak mümkündür. Özellikle, iki kenar ve aralarındaki açıyı bildiğimizde aşağıdaki formül kullanılabilir:
Burada, a ve b kenar uzunluklarını, C ise bu kenarlar arasındaki açıyı temsil etmektedir. 4. Uygulamalar ve Örnekler Üçgen alan hesaplama, birçok alanda uygulama bulmaktadır. İnşaat mühendisliği, mimari tasarım, arazi ölçümü gibi alanlarda sıkça kullanılan bir yöntemdir. Örnek vermek gerekirse, bir inşaat projesinde üçgen alan hesaplama, malzeme miktarını belirlemek için kritik öneme sahiptir. 5. Ek Bilgiler Üçgen alan hesaplamanın yanı sıra, üçgenin çevresi gibi diğer geometrik özellikleri de hesaplamak mümkündür. Üçgenin çevresi, kenar uzunluklarının toplamı ile bulunur:
Bunun yanı sıra, üçgenin iç açılarının toplamı her zaman 180 derece olduğundan, üçgenle ilgili hesaplamalar yaparken bu bilgi de göz önünde bulundurulmalıdır. Sonuç olarak, üçgen alan hesaplama, matematiksel ve pratik açıdan önemli bir konudur. Üçgenin alanını hesaplamak için farklı yöntemlerin kullanılması, bu geometrik şekil ile ilgili daha derin bir anlayışa sahip olmayı sağlar. |












































Üçgende eğim hesaplama, genellikle geometri derslerinde karşılaştığımız bir kavram. Eğim, bir üçgenin kenarlarının yatayla yaptığı açıyı belirler. Bu hesaplamalar, özellikle mühendislik ve mimarlıkta önemli bir yer tutar. Üçgende eğim hesaplama yöntemlerini öğrenmek, uygulamalarda büyük fayda sağlıyor.
Merhaba Özertan,
Üçgende eğim hesaplama konusuna değindiğin için teşekkürler. Bu kavram, gerçekten de geometri derslerinde önemli bir yer tutuyor ve birçok alanda, özellikle mühendislik ve mimarlıkta, pratik uygulamalara katkı sağlıyor.
Eğim Hesaplama Yöntemleri üzerine daha fazla bilgi edinmek, bu tür hesaplamaları doğru bir şekilde yapabilmek için oldukça faydalı. Mesela, üçgenin kenar uzunluklarını bilmek, eğimi hesaplamak için gerekli bir başlangıç noktası. Ayrıca, trigonometrik oranları kullanarak açılar üzerinden de eğim hesaplamak mümkündür.
Uygulama Alanları açısından bakıldığında, eğim hesaplamalarının yapıldığı birçok proje var. Yollar, binalar ve çeşitli yapısal tasarımlar bu hesaplamalara dayanarak oluşturuluyor. Bu nedenle, eğim hesaplama becerilerini geliştirmek, gelecekteki projelerde büyük avantaj sağlayabilir.
Bu konudaki düşüncelerini ve deneyimlerini paylaşman, diğerlerinin de bu alanda daha fazla bilgi edinmesine yardımcı olabilir. Tekrar teşekkürler!
Üçgen çevre hesaplama, üçgenin kenar uzunluklarının toplamı ile yapılır. Üçgenin kenarlarını bildiğinizde, çevresini kolayca bulabilirsiniz. Bu hesaplama, inşaat ve mimarlık gibi birçok alanda önemlidir. Üçgen çevre hesaplama yöntemleri, projelerdeki malzeme ihtiyaçlarını belirlemek için kritik öneme sahiptir.
Üçgen Çevre Hesaplama konusunda verdiğiniz bilgiler oldukça doğru ve faydalı. Üçgenin kenar uzunluklarının toplamı ile çevre hesabı yapılması, temel geometri bilgilerindendir ve pek çok alanda sıkça kullanılmaktadır.
Önemi açısından, özellikle inşaat ve mimarlık sektörlerinde projelerin planlanması aşamasında bu tür hesaplamaların yapılması, malzeme ihtiyacını belirlemek açısından kritik bir rol oynar. Doğru hesaplamalar, hem maliyet kontrolü sağlar hem de projelerin zamanında tamamlanmasına yardımcı olur.
Bu nedenle, üçgen çevre hesaplaması gibi temel matematiksel işlemleri bilmek, sadece akademik anlamda değil, pratikte de büyük bir avantaj sağlamaktadır. Elinize sağlık!
Üçgen alanı nasıl hesaplanır? Bu konuda farklı formüller ve yöntemler mevcut. Taban ve yükseklik ile hesaplama en yaygın olanı. Ayrıca kenar uzunlukları ile Heron formülü ve açıları kullanarak hesaplama da yapılabilir. Hangi yöntemin daha uygun olduğunu belirlemek önemli.
Üçgen Alan Hesaplama Yöntemleri
Çinel, üçgen alanını hesaplamak için doğru yöntemleri seçmek, duruma göre oldukça önemlidir. En yaygın kullanılan yöntemler arasında taban ve yükseklik ile hesaplama öne çıkmaktadır. Bu yöntem, üçgenin taban uzunluğunu ve yükseklik ölçüsünü bilmeniz durumunda oldukça pratik bir şekilde alanı bulmanızı sağlar.
Taban ve Yükseklik Yöntemi
Üçgenin alanını hesaplamak için kullanılan formül şu şekildedir:
\[ \text{Alan} = \frac{1}{2} \times \text{Taban} \times \text{Yükseklik} \]
Bu formül, üçgenin alanını hızlı bir şekilde bulmanın en basit yoludur.
Heron Formülü
Eğer üçgenin kenar uzunluklarını biliyorsanız, Heron formülü de etkili bir yöntemdir. Kenar uzunlukları \(a\), \(b\) ve \(c\) olan bir üçgen için alan şu şekilde hesaplanır:
\[ s = \frac{a + b + c}{2} \]
\[ \text{Alan} = \sqrt{s \times (s-a) \times (s-b) \times (s-c)} \]
Bu yöntem, kenar uzunluklarını bilmekle birlikte yükseklik ölçüsü olmayan durumlarda oldukça faydalıdır.
Açıları Kullanarak Hesaplama
Ayrıca, üçgenin açılarını kullanarak da alan hesaplanabilir. Örneğin, bir açı ve ona komşu iki kenar uzunluğu biliniyorsa, alan şu formül ile hesaplanabilir:
\[ \text{Alan} = \frac{1}{2} \times a \times b \times \sin(C) \]
Burada \(C\) açı, \(a\) ve \(b\) ise kenar uzunluklarıdır.
Sonuç olarak, hangi yöntemin daha uygun olduğu, elinizdeki verilere ve üçgenin özelliklerine bağlıdır. Her bir yöntem, farklı durumlar için avantajlar sunabilir. Bu nedenle, hangi bilgilerin mevcut olduğuna göre en uygun yöntemi seçmek önemlidir.
Üçgen kenar uzunluğu hesaplama konusunda farklı yöntemler mevcut. Kenar ve yükseklik kullanarak, iki kenar ve açı ile veya Heron formülü ile alan hesaplamak mümkün. Hangi yöntemin kullanılacağı, üçgenin türüne ve bilinen değerlerine bağlı olarak değişir. Bu yöntemler, üçgenin alanını doğru bir şekilde bulmamıza yardımcı olur.
Üçgen Alan Hesaplama Yöntemleri
Kanık, üçgen alanı hesaplamada farklı yöntemlerin bulunması, çeşitli durumlara uygun çözümler sunması açısından oldukça avantajlıdır. Her bir yöntemin kendine özgü kullanım alanları vardır.
Kenar ve Yükseklik Kullanarak Alan Hesaplama
Bu yöntem, üçgenin bir kenarının uzunluğuna ve o kenara ait yüksekliğine ihtiyaç duyar. Uygulaması oldukça basit olup, üçgenin alanını bulmak için "Alan = (kenar yükseklik) / 2" formülü kullanılır. Bu yöntem, kenar ve yükseklik değerlerinin kolayca ölçülebildiği durumlar için idealdir.
İki Kenar ve Açı Kullanarak Alan Hesaplama
Eğer üçgenin iki kenarı ve bu kenarların arasında kalan açı biliniyorsa, alanı hesaplamak için "Alan = (a b sin(C)) / 2" formülü kullanılabilir. Bu yöntem, açı ölçümlerinin ve kenar uzunluklarının bilindiği durumlarda etkili bir çözüm sunar.
Heron Formülü ile Alan Hesaplama
Heron formülü, üçgenin tüm kenar uzunlukları bilindiğinde kullanılır. Bu formül, "s = (a + b + c) / 2" ile yarı çevreyi hesapladıktan sonra "Alan = √(s (s - a) (s - b) (s - c))" şeklinde uygulanır. Heron formülü, özellikle kenarlar arasında farklı uzunluklar olduğunda oldukça kullanışlıdır.
Sonuç olarak, hangi yöntemin tercih edileceği, üçgenin türüne ve bilinen verilere bağlı olarak değişir. Bu sayede, üçgenlerin alanlarını doğru bir şekilde hesaplamak mümkün olur.
Üçgen alan hesaplama yöntemleri hakkında bilgi verirken, özellikle Heron formülünün ne kadar faydalı olduğuna dikkat çekmek isterim. Üçgenin kenar uzunluklarını bildiğimizde, bu formül sayesinde alanı kolayca hesaplayabiliyoruz. Ancak, iki kenar ve aralarındaki açıyı kullanarak alan hesaplamak da oldukça pratik bir yöntem. Peki, bu yöntemlerin hangisini kullanırken hangi faktörleri göz önünde bulundurmalıyız? Örneğin, üçgenin tipine göre seçim yapmak önemli mi?
Üçgen Alan Hesaplama Yöntemleri
Üçgen alanını hesaplamak için çeşitli yöntemler bulunmaktadır ve bu yöntemlerin her birinin kendine özgü avantajları vardır. Özellikle Heron formülünün sağladığı kolaylık, kenar uzunluklarını bildiğimiz durumlarda alan hesaplamada büyük bir avantaj sunar. Heron formülü, üçgenin kenar uzunluklarını kullanarak alanı bulmamızı sağlar ve bu da özellikle kenar uzunluklarının bilindiği durumlarda pratik bir çözüm sunar.
İki Kenar ve Açı Yöntemi
Diğer taraftan, iki kenar ve aralarındaki açıyı kullanarak alan hesaplamak da oldukça etkili bir yöntemdir. Bu yöntem, özellikle açının ölçüsünü de bildiğimiz durumlarda, pratik bir yol olarak öne çıkar.
Yöntem Seçiminde Dikkat Edilmesi Gereken Faktörler
Yöntemlerin seçiminde dikkat edilmesi gereken bazı faktörler vardır. Öncelikle, üçgenin tipi önemlidir; dik üçgen, eşkenar üçgen ya da diğer türlerde farklı yöntemlerin uygulanması gerekecektir. Ayrıca, elimizdeki verilerin türü de seçimimizi etkiler. Örneğin, kenar uzunlukları biliniyorsa Heron formülü kullanmak en mantıklısı olurken, açı bilgisi varsa, iki kenar ve açı yöntemini tercih etmek daha uygun olabilir.
Sonuç olarak, her iki yöntem de farklı durumlarda pratik çözümler sunar. Üçgenin özelliklerine göre uygun yöntemi seçmek, hesaplamaların doğruluğunu ve kolaylığını artıracaktır.