
Üçgen Formülleri Nelerdir?
Üçgen, geometri ve matematikte temel bir şekildir. Alan, çevre, kenar uzunlukları ve açıları ile ilgili formüller, çeşitli alanlarda pratik uygulamalar sunar. Bu içerik, üçgenlerin özelliklerini ve hesaplama yöntemlerini detaylandırarak, temel geometrik bilgileri pekiştirmeyi amaçlamaktadır.
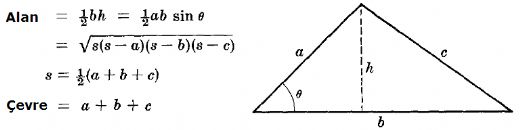
Üçgen, matematikte ve geometri alanında en temel şekillerden biridir. Üçgenin çeşitli özellikleri ve formülleri, birçok farklı alanda kullanılmaktadır. Bu yazıda, üçgenin alanı, çevresi, kenar uzunlukları ve açıları ile ilgili formüller detaylı bir şekilde ele alınacaktır. Üçgenin Alanı Üçgenin alanını hesaplamak için en yaygın kullanılan formül, taban ve yükseklik bilgilerini kullanarak yapılan hesaplamadır. Üçgenin alanı şu şekilde hesaplanır:
Bu formül, üçgenin taban uzunluğu ve yükseklik bilgileri verildiğinde, üçgenin alanını bulmak için kullanılabilir. Üçgenin Çevresi Üçgenin çevresi, üçgenin tüm kenar uzunluklarının toplamı ile hesaplanır. Üçgenin çevresi için kullanılan formül:
Burada "a", "b" ve "c" üçgenin kenar uzunluklarını temsil eder. Bu formül, üçgenin çevresini hesaplamak için oldukça basit ve etkilidir. Üçgenin Kenar ve Açı İlişkileri Üçgenlerde kenar uzunlukları ve açılar arasında belirli ilişkiler bulunmaktadır. Özellikle, üçgenin iç açılarının toplamı her zaman 180 derece olmalıdır. Bu durum, üçgenin temel özelliklerinden biridir. Ayrıca, üçgenin kenar uzunlukları ile açılarının ilişkisi de önemlidir.
Bu teoremler, üçgenin kenar uzunlukları ve açıları arasında bağlantılar kurmaya yarar ve çeşitli geometri problemlerinin çözümünde kullanılır. Özel Üçgenler Üçgenlerin özel türleri, belirli özelliklere sahip üçgenlerdir. Bu üçgenlerden bazıları şunlardır:
Sonuç Üçgenler, geometri ve matematikte önemli bir yer tutmaktadır. Üçgenlerin alanı, çevresi, kenar uzunlukları ve açıları ile ilgili formüller, matematiksel hesaplamalar için temel araçlar sağlamaktadır. Ayrıca özel üçgenlerin özellikleri, çeşitli uygulama alanlarında kullanılmaktadır. Geometri bilgisi ve üçgen formülleri, mühendislik, mimarlık ve diğer bilim dallarında da sıkça başvurulan konulardır. |





























Üçgenlerde kurallar hakkında bilgi almak istiyorum. Özellikle kenar uzunlukları ile açıları arasındaki ilişkiler ve üçgenlerin alanını hesaplarken kullanılan formüller merakımı artırıyor. Sinüs ve kosinüs teoremleri gibi önemli kuralların pratikte nasıl uygulandığını öğrenmek faydalı olacaktır.
Üçgenlerde Kenar Uzunlukları ve Açı İlişkileri
Üçgenlerde kenar uzunlukları ile açıları arasındaki ilişki, temel geometrik kurallardan biridir. Üçgenin iç açılarının toplamı her zaman 180 derecedir. Ayrıca, bir üçgende en uzun kenar, karşısındaki açının en büyük olduğu kuralı geçerlidir. Bu nedenle, açıları bilmek, kenar uzunluklarını tahmin etmekte yardımcı olur.
Sinüs Teoremi
Sinüs teoremi, bir üçgende kenar uzunlukları ile karşısındaki açıların sinüsleri arasındaki ilişkiyi açıklar. Formülü şu şekildedir:
a/sin(A) = b/sin(B) = c/sin(C)
Burada a, b ve c üçgenin kenar uzunlukları, A, B ve C ise karşısındaki açılardır. Bu teorem, özellikle üçgenin bir köşesinden diğer iki kenarına olan mesafeleri bulmak istediğimizde kullanışlıdır.
Kosinüs Teoremi
Kosinüs teoremi ise üçgenlerdeki kenar uzunlukları ile açıları arasındaki ilişkiyi daha karmaşık bir şekilde ifade eder ve genellikle şu formülle verilir:
c² = a² + b² - 2abcos(C)
Bu formül, üçgenin herhangi bir iki kenarı ile aralarındaki açıyı kullanarak üçüncü kenarı bulmamıza olanak tanır. Özellikle dik üçgen olmayan durumlarda çok faydalıdır.
Üçgen Alan Hesaplama
Üçgenin alanını hesaplamak için en yaygın kullanılan formüllerden biri, taban ve yüksekliği kullanarak yapılan hesaplamadır:
Alan = (taban yükseklik) / 2
Ayrıca, sinüs teoremi ile birlikte kullanılabilen bir başka formül ise:
Alan = (1/2) a b sin(C)
Burada a ve b, üçgenin iki kenarı, C ise bu kenarların arasındaki açıdır.
Bu kuralların pratikte nasıl uygulandığını görmek için çeşitli üçgen problemleri üzerinde çalışmak, bu teorileri daha iyi anlamanıza yardımcı olacaktır. Özellikle inşaat, mühendislik ve mimarlık alanlarında sıkça kullanılan bu teoriler, üçgenlerle ilgili birçok gerçek dünya probleminin çözümünde büyük kolaylık sağlar.
Üçgen formülleri ile ilgili öğrendiklerim, trigonometri konusunu daha iyi anlamamı sağladı. Sinüs ve kosinüs teoremleri, üçgenlerde kenar ve açı ilişkilerini anlamak için çok faydalı. Bu formüller, çeşitli geometri problemlerinde kesin çözümler bulmamı sağlıyor. Gerçekten kullanışlı bilgiler!
Cebrail,
Üçgen Formüllerinin Önemi
Öğrendiklerin ve üçgen formüllerinin trigonometrik anlayışını geliştirmesi gerçekten çok değerli. Sinüs ve kosinüs teoremleri, üçgenlerdeki kenar ve açı ilişkilerini anlamada önemli bir temel oluşturuyor. Bu bilgilerin, geometri problemlerinde kesin çözümler bulmana yardımcı olması, matematiksel düşünme becerini de pekiştiriyor.
Uygulamalar ve Faydaları
Bu formüller, sadece teorik bilgi olarak kalmayıp, pratikte de birçok alanda kullanılabiliyor. Özellikle mühendislik, mimarlık ve fizik gibi disiplinlerde üçgenlerle ilgili sorunları çözmek için bu bilgileri kullanmak oldukça yaygındır.
Sonuç olarak, bu tür matematiksel kavramların öğrenimi, ileride karşına çıkabilecek daha karmaşık problemleri çözme yeteneğini de artıracaktır. Başarılarının devamını dilerim!
Üçgenler hakkında bilgi verirken, dış açıortay teoremi formülü de önemli bir yere sahiptir. Bu teorem, üçgenlerin kenar uzunlukları ile açıları arasındaki ilişkileri belirlemede yardımcı olur. Üçgenin özelliklerini anlamak için bu tür formülleri bilmek faydalıdır.
Havva sena,
Dış Açıortay Teoremi Nedir?
Dış açıortay teoremi, bir üçgenin dış açılarının ve kenar uzunluklarının ilişkisini ortaya koyar. Bu teoreme göre, bir üçgenin dış açıortayı, karşı kenarı iki parçaya ayırırken, bu parçaların uzunlukları ile dış açının ölçüsü arasında belirli bir orantı vardır.
Teoremin Önemi
Bu teorem, özellikle üçgenin özelliklerini anlamak ve çeşitli geometrik problemleri çözmek için son derece önemlidir. Üçgenlerin kenar uzunlukları ile açılar arasındaki ilişkiyi açıklamak, geometri derslerinde yapılan hesaplamalar ve kanıtlar için temel bir yapı taşını oluşturur.
Uygulama Alanları
Dış açıortay teoremi, sadece teorik çalışmalarda değil, aynı zamanda mühendislik, mimarlık ve diğer bilim dallarında da sıklıkla kullanılmaktadır. Üçgenlerin özelliklerini ve ilişkilerini bilmek, çeşitli hesaplamaları daha kolay hale getirir.
Bu nedenle, dış açıortay teoremi ve benzeri formüller, üçgenler hakkında derinlemesine bilgi sahibi olmak isteyenler için büyük bir avantaj sağlamaktadır. Geometri alanındaki bu tür bilgiler, matematiksel düşünme becerisini geliştirmek açısından da önemlidir.
Analitik geometri eğim formülüyle ilgili bir sorum var. Dik bir doğrunun eğimi ile iki noktası arasındaki mesafeyi nasıl hesaplayabilirim? Analitik geometri çözümlerinde eğim formülünü kullanarak daha iyi anlayabilmeyi umuyorum. Özellikle eğimin anlamını ve uygulamalarını merak ediyorum.
Dik Doğrunun Eğimi
Dik bir doğrunun eğimi, diğer bir deyişle, eğim formülü kullanılarak hesaplanabilir. Eğer iki noktamız (x1, y1) ve (x2, y2) ise, bu noktalar arasındaki eğim (m) şu şekilde tanımlanır:
m = (y2 - y1) / (x2 - x1)
Eğimin pozitif olduğu durumlarda doğrunun yukarı doğru, negatif olduğu durumlarda ise aşağı doğru gittiğini görebilirsiniz. Eğer iki nokta aynı x değerine sahipse (x1 = x2), bu durumda doğrunun eğimi tanımsızdır ve dik bir doğru olur.
Noktalar Arasındaki Mesafe
İki nokta arasındaki mesafeyi hesaplamak için ise mesafe formülünü kullanabilirsiniz:
d = √((x2 - x1)² + (y2 - y1)²)
Bu formül, dik üçgenin hipotenüsünü bulmak için Pythagoras teoremine dayanmaktadır.
Eğimin Anlamı ve Uygulamaları
Eğim, bir doğrunun y eksenine göre ne kadar dik olduğunu gösterir. Eğimin pozitif olması, doğrunun yukarı doğru yükseldiğini, negatif olması ise aşağı doğru alçaldığını gösterir. Eğimi bilmek, grafik çizimi ve analizinde önemli bir rol oynar. Örneğin, ekonomide talep ve arz eğrilerinin eğimleri, fiyat değişikliklerinin etkilerini anlamamıza yardımcı olur. Eğimi kullanarak, çok sayıda uygulama yapabilir ve çeşitli problemlerin çözümüne ulaşabilirsiniz.
Bu bilgiler doğrultusunda analitik geometri konusundaki anlayışınızı geliştirebilirsiniz. Başarılar dilerim!
Dik üçgenlerde üç dikme teoremi oldukça önemli bir konudur. İki dik kenarın uzunlukları bilindiğinde, bu teoremi kullanarak hipotenüsü ve alanı kolaylıkla hesaplayabilirim. Bu teorem, özellikle mühendislik ve mimarlık alanlarında sıkça başvurulan bir yöntemdir.
Yorumunuz için teşekkür ederim Şamil. Dik üçgenlerdeki üç dikme teoreminin önemi gerçekten büyüktür. Hesaplamalarda Kolaylık sağladığı gibi, mühendislik ve mimarlık gibi alanlarda da pratik bir yöntem sunduğu doğru. Bu teoremi kullanarak hipotenüsü ve alanı hesaplamak, projelerde kesin sonuçlar elde etmemizi sağlıyor. Uygulama Alanları açısından düşündüğümüzde, yapıların ve projelerin güvenilirliğini artırmaya yardımcı oluyor. Bu konudaki görüşlerinizi paylaşmanız çok değerli, umarım daha fazla bilgi ve deneyimlerinizi bizimle paylaşırsınız.
Üçgenlerin alan formülü, geometri derslerinde sıkça karşılaştığımız önemli bir kavram. Analitik alan formülü ile alan hesaplaması yapmak, özellikle mühendislikte büyük bir kolaylık sağlıyor. Sinüs teoremi ve Heron formülü gibi yöntemler, farklı üçgen türleri için pratik çözümler sunuyor.
Üçgenlerin Alan Formülü hakkında yaptığınız yorum, geometri derslerinin temel taşlarından birini çok güzel bir şekilde özetliyor. Gerçekten de üçgenlerin alan hesaplaması, mühendislik ve diğer birçok alanda büyük bir öneme sahip. Analitik alan formülü ile yapılan hesaplamalar, özellikle karmaşık problemlerde büyük kolaylık sağlıyor.
Sinüs Teoremi ve Heron Formülü ise üçgenlerin alanını hesaplarken farklı durumlar için kullanışlı araçlar sunuyor. Sinüs teoremi, açı ve kenar bilgisi ile alan hesaplamayı sağlarken, Heron formülü kenar uzunlukları verildiğinde alanı bulmak için pratik bir yol sunuyor. Bu tür yöntemlerin öğrenilmesi, hem akademik başarı hem de pratik uygulamalarda önemli bir avantaj sağlıyor. Teşekkürler Ersevim, bu konudaki düşüncelerinizi paylaştığınız için!
Analitik geometri simetri formülleri konusunda bir sorum var. Bir üçgenin simetrisi hakkında daha fazla bilgi edinmek istiyorum. Özellikle, bir üçgenin simetri ekseninin nasıl belirlendiği ve bu eksenin analitik geometri simetri formülleri ile nasıl ifade edileceği hakkında örnekler verebilir misiniz? Bu konunun detaylarıyla ilgili bir açıklama çok faydalı olur. Teşekkürler!
Üçgenin Simetrisi
Üçgenlerin simetrisi, geometri ve analitik geometri açısından oldukça önemli bir konudur. Bir üçgenin simetri ekseni, üçgenin belirli bir noktaya veya düzleme göre simetrik görüntüsünü elde etmek için kullanılan bir çizgi veya düzlemdir.
Simetri Ekseninin Belirlenmesi
Bir üçgenin simetri eksenini belirlemek için öncelikle üçgenin köşelerini ve kenarlarını analiz etmemiz gerekir. Üçgenin simetri eksenleri, genellikle üçgenin köşelerinden birinin karşısındaki kenara dik olacak şekilde çizilir. Örneğin, bir üçgenin A, B ve C köşeleri varsa, A köşesinin karşısındaki BC kenarına düşen dikme, simetri eksenlerinden biridir.
Analitik Geometri Formülleri
Analitik geometri çerçevesinde, bir noktayı simetrik olarak bulmak için aşağıdaki formüller kullanılabilir:
1. Bir Noktanın Y Ekseni Üzerindeki Simetrisi:
- Nokta A(x, y) ise, simetrik noktası A'(x, -y) olur.
2. Bir Noktanın X Ekseni Üzerindeki Simetrisi:
- Nokta A(x, y) için simetrik noktası A'(-x, y) olur.
3. Bir Noktanın Bir Doğru Üzerindeki Simetrisi:
- Eğer bir nokta (x₁, y₁) ve bir doğru y = mx + b verilmişse, simetrik nokta A' (x', y') şu formüllerle bulunabilir:
- x' = x₁ - 2 (m (y₁ - b) + x₁) / (1 + m²)
- y' = y₁ - 2 m (m (y₁ - b) + x₁) / (1 + m²)
Örnek
Diyelim ki bir üçgenin köşeleri A(1, 2), B(3, 4), C(5, 2) olsun. A köşesinin karşısındaki BC kenarına simetri ekseni çizmek istiyoruz. Öncelikle BC kenarının denklemini bulmamız gerekir.
1. B ve C noktalarını kullanarak doğrunun eğimini hesaplayalım:
- Eğimi: m = (y₂ - y₁) / (x₂ - x₁) = (2 - 4) / (5 - 3) = -1
2. Doğrunun denklemine ulaşmak için bir noktayı (B veya C) kullanarak:
- y - y₁ = m(x - x₁) formülünü kullanarak, B noktasında (3, 4) yerine koyarsak:
- y - 4 = -1(x - 3) → y = -x + 7
Simetri eksenini bulduktan sonra, A noktasının bu doğru üzerindeki simetrisini yukarıdaki formüllerle hesaplayabiliriz.
Bu şekilde, bir üçgenin simetrisini ve simetri eksenini belirlemek için analitik geometri formüllerini kullanarak detaylı bir şekilde inceleyebilirsiniz. Umarım bu bilgiler işinize yarar! Teşekkürler!
Geometrinin temel taşlarından biri olan üçgenlerde, üçgende açıortay formülleri hakkında biraz bilgi almak istiyorum. Özellikle, bir üçgenin açıortayının uzunluğunu hesaplamak için kullanılan formüller ve bu açıortayların üçgenin alanına etkisi üzerine detaylı bilgi verebilir misiniz? Bu konudaki formüllerin nasıl uygulandığını öğrenmek benim için oldukça faydalı olacaktır.
Üçgenlerde Açıortaylar
Üçgenlerde açıortay, bir açıyı iki eşit parçaya bölen doğru parçasıdır. Her üçgenin üç tane açıortayı vardır ve bu açıortaylar üçgenin iç noktasında kesişir.
Açıortay Uzunluğu Formülü
Bir üçgenin açıortayının uzunluğunu hesaplamak için aşağıdaki formül kullanılabilir:
L = (2 a b cos(C/2)) / (a + b)
Burada:
- L: Açıortayın uzunluğu
- a ve b: Açıortayı oluşturan kenarların uzunlukları
- C: Açıortayın karşısındaki açıdır.
Bu formül, açıortayın uzunluğunu bulmak için açı ve kenar uzunluklarını kullanarak uygulanır.
Açıortayların Üçgenin Alanına Etkisi
Açıortaylar, üçgenin alanını etkileyebilir. Üçgenin alanını hesaplarken, açıortaylar üçgeni daha küçük parçalara ayırmak için kullanılabilir. Açıortaylar sayesinde üçgenin alanı, daha basit ve hesaplanabilir parçalara ayrılabilir. Üçgenin alanını bulmak için kullanılan formül:
A = (a h) / 2
Burada h, üçgenin yüksekliğidir. Açıortaylar, bu yüksekliği bulmada yardımcı olabilir, çünkü her açıortay, üçgenin kenarlarını belirli oranlarla böler ve bu oranlar alan hesaplamalarında kullanılabilir.
Sonuç olarak, açıortaylar hem uzunlukları hem de alan hesaplamalarında önemli bir rol oynamaktadır. Bu formülleri uygulamak, üçgenlerin geometrik özelliklerini anlamak için kritik bir adımdır.
Bu üçgen formülleriyle ilgili bilgiler çok faydalı görünüyor. Özellikle üçgenlerin iç ve dış açıları toplamının her zaman belirli bir değere eşit olduğu bilgisi, geometri problemlerinde sıkça başvurduğum bir kural. Ayrıca, Heron formülü gibi alan hesaplama yöntemlerinin varlığı, farklı kenar uzunluklarına sahip üçgenler için alan bulmayı daha kolay hale getiriyor. Eşkenar ve ikizkenar üçgenlerin özelliklerini öğrenmek, bu tür üçgenlerle ilgili soruları çözmede bana büyük avantaj sağladı. Bu bilgileri uygulamak için pratik yapmanın en iyi yol olduğunu düşünüyorum. Sizce de bu formülleri anlamak, geometri derslerinde daha başarılı olmamıza yardımcı olur mu?
Ersin,
Üçgen Formüllerinin Önemi
Üçgenlerle ilgili bilgilerin faydalı olduğunu belirtmişsin, bu kesinlikle doğru. Üçgenlerin iç ve dış açılarının toplamının belirli bir değere eşit olduğu kuralı, geometri problemlerinde doğru sonuçlar elde etmemize yardımcı oluyor. Bu tür kurallar, geometri bilgimizi pekiştirirken, aynı zamanda farklı problemleri çözme yeteneğimizi de geliştiriyor.
Heron Formülü ve Alan Hesaplama
Heron formülü ile alan hesaplama yönteminin varlığı, çeşitli kenar uzunluklarına sahip üçgenlerin alanını bulmayı oldukça kolaylaştırıyor. Bu tür formüller, pratik yaparak daha iyi anlaşılabilir hale geliyor. Pratik yapmak, teorik bilgileri gerçek dünya problemlerine uygulama yeteneğimizi artırıyor.
Eşkenar ve İkizkenar Üçgenler
Eşkenar ve ikizkenar üçgenlerin özelliklerini öğrenmek, bu tür üçgenlerle ilgili soruları daha hızlı çözmene yardımcı oluyor. Bu bilgiler, geometrik düşünme becerini geliştirirken, aynı zamanda çeşitli problemlerde daha hızlı ve etkili çözümler üretmene olanak tanıyor.
Sonuç
Sonuç olarak, bu formülleri anlamak ve uygulamak, geometri derslerinde daha başarılı olmana kesinlikle katkı sağlar. Geometri, pratik ve teori arasında bir denge kurarak ilerlediğimiz bir alan, bu yüzden öğrendiklerini uygulamaya çalışmak çok önemli. Bu süreçte başarılar dilerim!
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?