
Üçgen Eşitsizliği Üçgende Kenarları Hesaplama
Üçgen eşitsizliği, üçgenin kenar uzunlukları arasındaki temel ilişkileri belirler ve bu ilişkiler, bir üçgenin varlığını sağlamak için gereklidir. Bu kavram, geometri ve matematikte önemli bir yer tutar ve çeşitli alanlarda uygulamalara sahiptir.
Üçgen Eşitsizliği Üçgen eşitsizliği, geometri ve matematikte önemli bir kavramdır. Bu eşitsizlik, herhangi bir üçgende, her iki kenarın toplamının üçüncü kenardan büyük olduğunu ifade eder. Üçgen eşitsizliği, üçgenin kenar uzunlukları a, b ve c ile ifade edilir. Bu bağlamda, üçgen eşitsizlikleri şu şekilde tanımlanabilir:
Bu üç eşitsizlik, bir üçgenin kenar uzunluklarının geçerliliğini sağlamaktadır. Eğer bu eşitsizliklerden biri sağlanmıyorsa, verilen kenar uzunlukları ile bir üçgen oluşturmak mümkün değildir. Üçgenin Kenarlarının Hesaplanması Üçgenin kenar uzunluklarının hesaplanması, çeşitli geometrik yöntemler ve formüller kullanılarak gerçekleştirilebilir. Bu hesaplamalar, üçgenin tipine, kenar uzunluklarına ve açılarına bağlı olarak değişkenlik gösterir. Üçgenin kenar uzunluklarını hesaplama yöntemlerinden bazıları şunlardır:
Bu formüller, üçgenin kenar uzunluklarını hesaplamak için farklı durumlarda kullanılabilir. Üçgenin özelliklerine ve verilen bilgilere bağlı olarak en uygun yöntem seçilmelidir. Uygulamalar ve Örnekler Üçgen eşitsizliği ve kenar uzunluklarının hesaplanması, birçok alanda önemli bir yere sahiptir. Özellikle mühendislik, mimarlık ve fizik gibi disiplinlerde sıklıkla karşımıza çıkar. Örneğin, bir inşaat projesinde üçgen eşitsizliğini kullanarak, yapı elemanlarının güvenliğini sağlamak mümkündür.Ayrıca, üçgen kenar uzunlukları hesaplanırken, aşağıdaki örnek üzerinden gidilebilir: Verilen bir üçgenin kenar uzunlukları a = 3, b = 4, c = 5 olsun. Bu durumda, üçgen eşitsizliklerinin kontrolü:
Bu durumda, verilen kenar uzunlukları ile bir üçgen oluşturmak mümkündür. Sonuç Üçgen eşitsizliği, geometri alanında temel bir prensip olup, üçgenin kenar uzunlukları arasında belirli bir ilişki olduğunu ortaya koyar. Bu eşitsizliklerin sağlanması, üçgenin varlığı için gereklidir. Üçgen kenar uzunluklarının hesaplanması ise farklı yöntemler ve teoremler kullanılarak gerçekleştirilebilir. Bu temel bilgiler, matematiksel ve mühendislik uygulamalarında önemli bir yer tutmaktadır. Ek olarak, üçgen eşitsizliğinin daha ileri düzeyde incelenmesi, çokgenlerin ve daha karmaşık geometrik şekillerin analizine olanak tanır. Bu nedenle, üçgen eşitsizliğini anlamak ve uygulamak, matematiksel düşünme becerisini geliştirmek için kritik bir adımdır. |
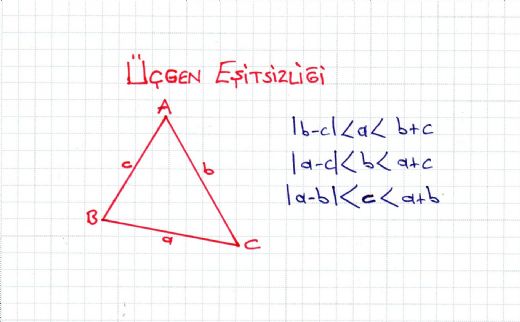















































Kenarlardan biri, diğer iki kenarın toplamından küçük ama farkından büyük olmadığında üçgen oluşmadığını nasıl kontrol edebilirim?
Tokyürek, üçgen oluşturma koşullarını kontrol etmek için üçgen eşitsizliği teoremini kullanabilirsin. Bu teoreme göre, bir üçgenin kenar uzunlukları a, b ve c ise, şu üç koşulun hepsinin sağlanması gerekir:
1. a + b > c
2. a + c > b
3. b + c > a
Aynı zamanda, hiçbir kenar diğer iki kenarın farkından büyük olmamalıdır:
1. |a - b| < c
2. |a - c| < b
3. |b - c| < a
Bu koşulları kullanarak, verilen kenar uzunluklarının bir üçgen oluşturup oluşturmadığını kontrol edebilirsin. Bu eşitsizliklerin hepsinin sağlanması durumunda bir üçgen oluşturulabilir. Eğer herhangi biri sağlanmıyorsa, üçgen oluşturulamaz.