
Üçgenin Köşegenleri
Üçgen, geometrinin temel şekillerinden biri olup üç kenar ve üç köşeden oluşur. Kendi içerisinde kösegen kavramı geçerli olmamakla birlikte, üçgenlerin temel özellikleri ve yapıları matematiksel analizlerde önemli bir yer tutar. Bu çalışma, üçgenlerin özelliklerini ve kullanımlarını ele almaktadır.
Üçgenin Köşegenleri Üçgen, geometrinin temel şekillerinden biri olup, üç kenar ve üç köşeden oluşur. Üçgenin köşegenleri, genellikle çokgenlerde ele alınan bir kavramdır. Üçgen özel birçokgen türü olduğu için, köşegen kavramı üçgen için geçerli değildir. Bu makalede, üçgenin temel özellikleri, kenarları ve köşeleri hakkında detaylı bilgi verilecek ve köşegen kavramının üçgen üzerindeki etkileri ele alınacaktır. 1. Üçgenin Temel Özellikleri Üçgenler, kenar uzunlukları ve iç açıları ile tanımlanır. Üçgenin temel özellikleri şunlardır:
2. Üçgen Türleri Üçgenler, kenar uzunlukları ve açı büyüklüklerine göre farklı türlere ayrılabilir:
3. Üçgenin Kenarları ve Köşeleri Bir üçgenin üç kenarı ve üç köşesi vardır. Kenarlar, üçgenin dış hatlarını oluştururken, köşeler üçgenin açılarının kesişim noktalarıdır. Üçgenin kenarları ve köşeleri ile ilgili bazı önemli noktalar şunlardır:
4. Köşegen Kavramı ve Üçgenler Köşegen, birçokgenin iki köşesini birleştiren doğru parçasıdır. Üçgen, yalnızca üç köşe ve üç kenara sahip olduğu için, köşegen kavramı burada uygulanamaz. Ancak, çokgenler arasında yapılan bazı karşılaştırmalar ve analizlerde köşegenler önemli bir rol oynar. Üçgenlerin özellikleri, diğer çokgenlerle kıyaslandığında daha sınırlı bir yapıdadır. 5. Üçgenin Önemi ve Kullanım Alanları Üçgenler, matematik ve geometri alanında önemli bir yere sahiptir. Mühendislikten mimariye, sanattan bilime kadar birçok alanda üçgenlerin kullanımı yaygındır. Üçgenlerin özellikleri, çeşitli problemleri çözmek için temel bir yapı sağlar. Özellikle:
Sonuç Üçgenler, köşegen kavramı açısından özel bir öneme sahip olmasa da, geometrinin temel taşlarından biridir. Üçgenlerin köşeleri ve kenarları, birçok matematiksel ve fiziksel olgunun anlaşılmasına yardımcı olur. Bu makalede, üçgenin temel özellikleri ve yapısı ele alınmış, üçgenin köşegenleri kavramı hakkında bilgi verilmiştir. Geometrik şekillerin derinlemesine anlaşılması, birçok disiplin için kritik bir öneme sahiptir. |
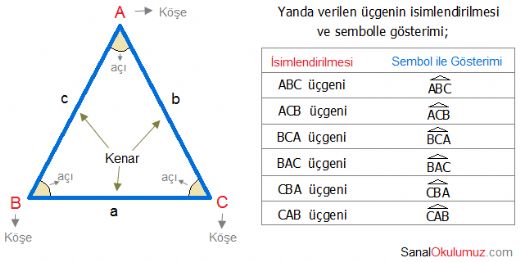















































Peki, üçgenin köşegenlerinin olmaması onun diğer çokgenlerden farklı özelliklere sahip olduğunu mu gösterir? Bu durum üçgenin geometri çalışmalarında nasıl bir önem taşır?
Merhaba Oray,
Üçgenin köşegenlerinin olmaması, onun diğer çokgenlerden belirli açılardan farklı olduğunu gösterir. Köşegenlerin olmayışı, üçgenin en basit ve en temel çokgen türü olmasından kaynaklanır. Bu durum, üçgenin geometri çalışmalarında kritik bir rol oynamasını sağlar. Üçgenler, birçok kompleks geometrik şeklin ve yapıların temel yapı taşlarıdır. Örneğin, poligonları üçgenlere bölerek alan hesaplamaları yapabiliriz. Üçgenlerin bu temel özellikleri, geometri ve trigonometri konularında önemli bir yere sahip olmalarına neden olur. Bu yüzden, üçgenlerin köşegenlerinin olmaması onların sadeliğini ve temel geometrik ilkeler içerisindeki önemini vurgular.
Saygılar,