
Üçgen Piramit
Üçgen piramit, üçgen tabana sahip ve üçgen yüzeylerden oluşan bir üç boyutlu geometrik şekildir. Matematik ve mimarlıkta önemli bir role sahip olan bu yapı, hacim ve yüzey alanı hesaplamalarıyla beraber çeşitli alanlarda incelenir. Özellikleri ve uygulamalarıyla dikkat çeker.
Üçgen Piramit Üçgen piramit, üçgen tabana sahip olan ve üçgen yüzeylerden oluşan bir üç boyutlu geometrik şekildir. Matematiksel ve mimari açıdan önemli bir yere sahip olan bu yapı, birçok bilim dalında yer bulmaktadır. Üçgen piramitler, özellikle geometri, yapı mühendisliği ve mimarlık alanlarında sıkça incelenmektedir. Tanım ve Özellikler Üçgen piramit, tabanı bir üçgen olan ve bu tabandan bir noktanın yukarıya doğru uzandığı bir şekildir. Üçgen piramitin bazı temel özellikleri şunlardır:
Bu özellikler, üçgen piramidin yapılandırılması ve analiz edilmesi açısından temel bir çerçeve sunar. Hacim ve Yüzey Alanı Hesaplamaları Üçgen piramidin hacmini ve yüzey alanını hesaplamak, geometri derslerinde önemli bir konudur. Hacim ve yüzey alanı hesaplamaları, çeşitli formüllerle gerçekleştirilir.
Bu hesaplamalar, mühendislik uygulamaları ve mimari tasarımlar için kritik öneme sahiptir. Geometrik ve Mimari Örnekler Üçgen piramitler, hem geometrik kurallara hem de estetik değerlere uygun birçok yapı ve tasarımda yer almaktadır. Öne çıkan bazı örnekler:
Bu örnekler, üçgen piramidin farklı alanlardaki önemini ve kullanımını göstermektedir. Sonuç Üçgen piramit, hem matematiksel hem de mimari açıdan önemli bir yapı olarak karşımıza çıkmaktadır. Hacim ve yüzey alanı hesaplamaları, bu piramidin çeşitli uygulamalarını desteklemekte ve mühendislik ile mimarlık alanlarında büyük bir rol oynamaktadır. Geometrik özellikleri ve mimari örnekleri ile üçgen piramit, bilim ve sanatta önemli bir yer tutmaktadır. Ekstra Bilgiler Üçgen piramidinin incelenmesi, sadece temel geometrik bilgilerle sınırlı kalmayıp, aynı zamanda çeşitli fiziksel ve mühendislik prensiplerini de içermektedir. Örneğin, üçgen piramidinin yapısal dayanıklılığı, malzeme bilimi ve yapı mühendisliği alanlarında önemli bir araştırma konusudur. Ayrıca, üçgen piramidinin simetrisi ve estetiği, sanatsal tasarımlarda ve mimaride sıkça dikkate alınmaktadır. Bu nedenle, üçgen piramitler, hem teorik hem de pratik açıdan zengin bir araştırma alanı sunmaktadır. |
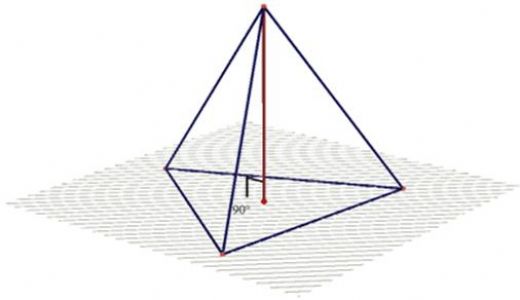















































Bu yazıda üçgen piramitin farklı türleri ve özellikleri oldukça iyi bir şekilde açıklanmış. Üçgen dik piramit ve üçgen eğik piramit arasındaki farkları anlamak için çok faydalı bilgiler verilmiş. Özellikle, dik piramidin tepe noktasının tabana dik olduğu durumun net bir şekilde tanımlanması, konuyu daha anlaşılır kılmış. Ayrıca, piramitlerin genel tanımı ve diğer piramit türleri ile ilgili bilgiler de oldukça bilgilendirici. Yükseklik ve hacim hesaplamaları gibi matematiksel kavramların da açıklanması, bu konuyla ilgilenenler için oldukça yararlı. Sizce bu tür geometrik yapıların öğrenilmesi, matematiğe olan ilgiyi artırır mı?
Banugül,
Üçgen Piramitlerin Öğrenilmesi konusundaki yazınız gerçekten kapsamlı ve bilgilendirici. Üçgen dik piramit ve üçgen eğik piramit arasındaki farkların net bir şekilde ortaya konması, konunun anlaşılmasını oldukça kolaylaştırıyor. Matematiksel kavramların, özellikle yükseklik ve hacim hesaplamalarının açıklanması ise, öğrencilerin bu geometrik yapıları daha iyi kavramalarına yardımcı olabilir.
Matematiğe İlgi Üzerine gelince, bu tür geometrik yapıların öğrenilmesinin matematiğe olan ilgiyi artıracağına inanıyorum. Geometri, soyut matematik kavramlarının somut birer temsilcisi olarak karşımıza çıkıyor. Üçgen piramit gibi yapılar, öğrencilerin matematiksel düşünme becerilerini geliştirmelerine ve problem çözme yeteneklerini artırmalarına yardımcı olabilir. Dolayısıyla, bu tür eğitici içeriklerin artması, matematiğe olan ilgiyi mutlaka olumlu yönde etkileyecektir.