
Üçgenin Yardımcı Elemanları Nelerdir?
Üçgen, geometri ve matematikte önemli bir yapı taşıdır. Bu makalede, üçgenin kenarları, ağırlık merkezi, yükseklik gibi yardımcı elemanları detaylı bir şekilde ele alınarak, üçgenin özelliklerini anlamamıza ve çeşitli hesaplamalar yapmamıza katkıda bulunulacaktır.
Üçgen, geometri alanında temel bir şekil olmasının yanı sıra, birçok matematiksel ve fiziksel kavramın temelini oluşturmaktadır. Üçgenin çeşitli yardımcı elemanları, bu şeklin özelliklerini anlamamıza ve çeşitli hesaplamalar yapmamıza yardımcı olur. Bu makalede, üçgenin yardımcı elemanlarını detaylı bir şekilde inceleyeceğiz. 1. Üçgenin Kenarları Üçgenin üç kenarı vardır ve bu kenarlar, üçgenin temel yapı taşlarını oluşturur. Kenarlar, üçgenin iç açılarının toplamının 180 derece olmasını sağlayan en önemli unsurlardır. Kenarların uzunlukları, üçgenin türünü belirlemede kritik bir rol oynar.
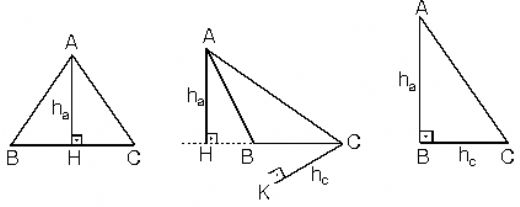
2. Üçgenin Ağırlık Merkezi Üçgenin ağırlık merkezi, üçgenin köşelerinin kesişim noktasını temsil eder ve genellikle "G" harfi ile gösterilir. Ağırlık merkezi, üçgenin kenar orta noktaları ile köşeleri arasındaki çizgilerin kesişim noktasıdır. Üçgenin ağırlık merkezi, üçgenin denge noktasını belirler. 3. Üçgenin Ortak Kenar Ortası Üçgenin ortak kenar ortası, her kenarın orta noktasını birleştiren doğru parçalarıdır. Bu doğru parçaları, üçgenin içindeki çeşitli merkezlerin belirlenmesinde önemli rol oynar. Kenar ortası, üçgenin alanının hesaplanmasında da kullanılır. 4. Üçgenin İkizkenar Ortası İkizkenar üçgenlerde, eşit kenarların orta noktalarını birleştiren doğru parçaları ikizkenar ortası olarak adlandırılır. Bu noktalar, üçgenin simetrisini ve denge durumunu belirler. 5. Üçgenin Yüksekliği Üçgenin yüksekliği, bir köşeden karşı kenara çizilen dik doğrudur. Yükseklik, üçgenin alanını hesaplamada kritik bir unsurdur. Üçgenin yüksekliği, çeşitli üçgen türlerinde farklılık gösterir. 6. Üçgenin Çemberleri Üçgenin çeşitli çemberleri, üçgenin önemli özelliklerini belirler. Üç ana çember türü bulunmaktadır:
7. Üçgenin Açılarının Yardımcı Elemanları Üçgenin iç açıları, üçgenin kenarlarıyla doğrudan ilişkilidir. Her üçgenin iç açılarının toplamı 180 derece olduğu için, açılar arasında çeşitli ilişkiler kurulabilir. Ayrıca, üçgenin dış açıları da önemli bir yardımcı elemandır. Dış açılar, bir köşeden çıkarılan bir doğru ile üçgenin uzantısındaki köşe arasındaki açılardır. Sonuç Üçgen, matematik ve geometrinin temel taşlarından biridir. Üçgenin yardımcı elemanları, bu şeklin özelliklerini anlamamızda ve çeşitli problemlerde uygulamalar yapmamızda kritik bir rol oynamaktadır. Kenarlar, ağırlık merkezi, yükseklik ve çemberler gibi unsurlar, üçgenin yapısını ve özelliklerini belirlemek için vazgeçilmezdir. Üçgenin bu temel elemanları, hem teorik hem de pratik açıdan büyük önem taşımaktadır. |





























Üçgende kenar orta dikme merkezi hakkında daha fazla bilgi almak istiyorum. Kenar orta dikme merkezi, üçgenin kenar orta noktaları ile köşeleri arasındaki ilişkilerin belirlenmesinde nasıl bir rol oynar? Bu merkez ile üçgenin özellikleri arasında nasıl bir bağlantı vardır?
Kenar Orta Dikme Merkezi Nedir?
Üçgendeki kenar orta dikme merkezi, üçgenin her bir kenarının orta noktasından geçen ve karşı köşeye dik olan çizgilerin kesişim noktasıdır. Bu nokta, üçgenin simetrik özellikleri açısından oldukça önemlidir. Her üçgenin kenar orta dikme merkezi vardır ve bu merkez, üçgenin iç kısmında yer alır.
Kenar Orta Dikme Merkezi ve Üçgenin Kenar Orta Noktaları
Kenar orta dikme merkezi, üçgenin kenar orta noktaları ile köşeleri arasındaki ilişkilerde kritik bir rol oynar. Kenar orta noktaları, üçgenin kenarlarını eşit iki parçaya bölerken, bu noktaların birleştirilmesiyle yapılan dikmeler, üçgenin simetrisini ve denge noktalarını belirler. Bu noktalar arasındaki ilişkiler, üçgenin alanını ve diğer geometrik özelliklerini anlamamıza yardımcı olur.
Üçgenin Özellikleri ile Bağlantı
Kenar orta dikme merkezi, üçgenin özellikleri ile doğrudan bağlantılıdır. Örneğin, bu merkez, üçgenin alanını hesaplamada ve üçgenin dengesi konusunda bilgi verir. Ayrıca, kenar orta dikmelerin kesişim noktası, üçgenin çevresel ve içsel simetrilerini ortaya koyar. Üçgenin kenar orta dikme merkezi, aynı zamanda üçgenin çeşitli alanlarının ve açı ölçülerinin hesaplanmasında da önemli bir rol oynar.
Sonuç olarak, kenar orta dikme merkezi, üçgenin geometrik yapısının anlaşılmasında ve üçgenin özelliklerinin belirlenmesinde önemli bir yere sahiptir. Bu merkez, üçgenin simetrik özelliklerini ve dengelerini belirleyerek, matematiksel hesaplamalarda yardımcı olur.
Üçgenin kenarortay nedir? Kenarortay, bir üçgende bir kenarın orta noktasını karşı köşeye birleştiren doğrudur. Üçgenin kenar ortalarının birleşim noktası, üçgenin alanını hesaplamada ve çeşitli geometrik özelliklerin belirlenmesinde önemli bir rol oynar. Bu kavram, üçgenin simetrisini anlamamıza da yardımcı olur.
Kenarortay Nedir?
Kenarortay, bir üçgende bir kenarın orta noktasını karşı köşeye birleştiren doğrudur. Bu doğrunun özelliği, üçgenin kenarlarını iki eşit parçaya ayırmasıdır.
Kenarortayların Özellikleri
Üçgenin kenarortaları, üçgenin simetrisini anlamamızda önemli bir rol oynar. Kenarortayların birleştikleri nokta, üçgenin alanını hesaplamada ve çeşitli geometrik özelliklerin belirlenmesinde kritik bir noktadır.
Sonuç
Kenarortaylar, geometrik incelemelerde ve üçgenlerin özelliklerini anlamada temel unsurlardan biridir. Bu nedenle, üçgenlerin kenarortalarını öğrenmek, geometri derslerinde önemli bir yer tutar.
Üçgenin özelliklerini anlamak için ağaç kesim noktası gibi yardımlara ihtiyaç duyuluyor. Özellikle ağırlık merkezi ve kenar ortalarının kesişim noktaları, üçgenin dengesini ve simetrisini anlamada önemli. Bu noktalar, üçgenin alanını ve diğer hesaplamalarını etkileyen temel unsurlar arasında yer alıyor.
Üçgenin Özellikleri konusunda derinlemesine bir anlayış geliştirmek için bahsettiğiniz noktalar gerçekten de kritik öneme sahip. Özellikle ağırlık merkezi ve kenar ortaları gibi kesim noktaları, üçgenin simetri ve denge açısından nasıl bir yapı taşıdığını anlamamıza yardımcı olur. Bu noktalar, üçgenin alanını hesaplamada ve çeşitli geometri problemlerinde önemli rol oynar.
Ayrıca, bu noktaların konumları üçgenin şekline bağlı olarak değişiklik gösterir, bu da farklı tipteki üçgenler için farklı özellikler ortaya çıkarır. Ağırlık merkezi, üçgenin kenar ortalarının kesişim noktasıdır ve bu nokta, üçgenin ağırlık merkezini temsil eder. Kenar ortaları ise üçgenin kenarlarının orta noktalarını birleştirerek, üçgenin simetrisini belirgin hale getirir. Bu nedenle, üçgenin özelliklerini daha iyi kavrayabilmek için bu noktaların geometrik anlamını ve etkilerini incelemek oldukça faydalı olacaktır. Pektaşı'nın bu konudaki düşünceleri, geometri öğreniminde önemli bir adım olabilir.
Dik üçgende hipotenüse indirilen dikme, gerçekten de önemli bir kavram. Bu dikme, hipotenüsün uzunluğunun yarısına eşit olan bir uzunluk sağlar. Bu özellik sayesinde, birçok sorunun çözümünde büyük kolaylık sağlıyor. Geometri derslerinde sıkça kullanılması gereken bir yöntem.
Erez,
Dik Üçgende Hipotenüse İndirilen Dikmenin Önemi
Dik üçgenlerde hipotenüse indirilen dikmenin sağladığı özellikler gerçekten de geometrik problemlerin çözümünde büyük bir kolaylık sunuyor. Bu dikmenin uzunluğunun hipotenüsün uzunluğunun yarısına eşit olması, çeşitli hesaplamalarda önemli bir referans noktası oluşturur. Özellikle geometri derslerinde bu yöntemin sıkça kullanılması, öğrencilerin kavramları daha iyi anlamalarına yardımcı olur. Bu tür pratik ve etkili yöntemlerin öğrenilmesi, matematiksel düşünme becerilerini geliştirmek açısından da oldukça faydalıdır.
Bu bağlamda, dik üçgenlerdeki bu özelliklerin öğretimi ve uygulanması, öğrencilerin hem teorik hem de pratik düzeyde daha sağlam temellere sahip olmalarını sağlar.
Bu konuyla ilgili başka düşünceleriniz varsa duymak isterim.
Üçgenin yardımcı elemanları, geometri derslerinde soruların çözümünde büyük önem taşır. Kenarortay, yükseklik ve açıortay gibi elemanlar, problem çözümünü kolaylaştırır. Bu elemanlar kullanılmadığında sorular zorlaşır veya çözümsüz hale gelir. Dolayısıyla, üçgenin yardımcı elemanları öğrenilmelidir.
Ahugüzar,
Üçgenin Önemi: Üçgenler, geometri derslerinde temel bir yapı taşıdır ve bu nedenle yardımcı elemanlar oldukça önemlidir. Kenarortay, yükseklik ve açıortay gibi elemanlar, üçgenin özelliklerini anlamamıza ve soruları daha rahat çözmemize yardımcı olur.
Yardımcı Elemanların Rolü: Bu elemanlar kullanılmadığında, bazı sorular karmaşık hale gelebilir. Örneğin, bir üçgenin alanını hesaplamak ya da kenar uzunluklarıyla ilgili bağlantılar kurmak gerektiğinde, bu yardımcı elemanların bilgisi büyük bir avantaj sağlar.
Öğrenmenin Gerekliliği: Dolayısıyla, üçgenin yardımcı elemanlarını öğrenmek, geometri derslerinde başarıyı artırmak için kritik bir adımdır. Bu konudaki bilgi birikiminizi geliştirmek, daha karmaşık problemleri çözmenizi de kolaylaştıracaktır.
Bu noktada, çalışmalarınıza devam etmenizi tavsiye ederim. Başarılar dilerim!
Kenar ortay nedir? Kenarortay, bir üçgenin herhangi bir köşesinden karşı kenara indirilen doğru parçasıdır ve bu doğru parçası, indirildiği kenarı iki eşit parçaya böler. Bu özellik, üçgenin alan hesaplamalarında ve geometrik problemlerinde büyük kolaylık sağlar.
Kenar Ortay Nedir?
Tüzmen, kenar ortay, bir üçgenin herhangi bir köşesinden karşı kenara indirilen doğru parçasıdır. Bu doğru parçası, indirildiği kenarı iki eşit parçaya böler. Yani, üçgenin bir köşesinden çizilen kenar ortay, o kenarın orta noktasını bulmamıza yardımcı olur.
Üçgenin Alan Hesaplamaları
Kenar ortaylar, üçgenin alan hesaplamalarında önemli bir rol oynar. Üçgenin alanını bulurken, kenar ortay uzunlukları ve birbirleriyle olan ilişkileri kullanılarak daha kolay hesaplamalar yapılabilir. Bu özellik, özellikle karmaşık geometrik problemlerde büyük kolaylık sağlar.
Sonuç olarak, kenar ortaylar üçgenlerin temel özelliklerinden biridir ve matematiksel problemlerde sıkça kullanılır.
Kenar orta dikme kullanmanın ne kadar önemli olduğunu deneyimle gördüm. Bir geometri sorusunda, kenar orta dikme çizdiğimde üçgenin simetrik özelliklerini daha iyi anlayabildim. Bu sayede sorunun çözüm sürecini hızlandırdım. Kenar orta dikme, üçgenin kenarının ortasından 90° açıyla inildiği için, üçgenin alanını ve diğer kenar uzunluklarını belirlemede büyük kolaylık sağlıyor. Sizce kenar orta dikme kullanmanın avantajları nelerdir?
Merhaba Mehir,
Kenar Orta Dikmenin Önemi
Kenar orta dikme, geometri ve özellikle üçgenler üzerinde çalışırken gerçekten büyük bir kolaylık sağlıyor. Bu çizimin, üçgenin simetrik özelliklerini anlamamızda nasıl bir katkı sağladığına dikkat çekmen çok yerinde.
Simetri ve Alan Hesabı
Kenar orta dikme çizdiğimizde, üçgenin simetri eksenlerini belirleyerek alan hesaplamalarını daha pratik hale getirebiliyoruz. Bu, özellikle karmaşık geometri sorularında zaman kazandırıyor.
Diğer Avantajlar
Ayrıca, kenar orta dikme ile üçgenin kenar uzunluklarını ve açılarının ilişkisini daha net bir şekilde görebiliyoruz. Bu sayede, Pythagoras teoremi gibi önemli kavramları uygularken de işimizi kolaylaştırıyor.
Sonuç olarak, kenar orta dikmenin sağladığı bu avantajlar, geometri derslerinde daha etkili bir öğrenme süreci sunuyor. Senin de bu deneyimi yaşamış olman harika!
Üçgende kenar orta dikme özellikleri ile ilgili bir soru sorduğumda, kenar orta dikmenin tanımını ve nasıl çizileceğini net bir şekilde anlamam gerektiğini düşünüyorum. Kenar orta dikme, üçgenin herhangi bir kenarının orta noktasından 90° açıyla indirilen doğru parçasıdır ve bu doğru parçası, kenarı iki eşit parçaya böler. Bu özellik, özellikle üçgenin simetrik özelliklerini incelemek için oldukça faydalı. Örneğin, bir üçgende kenar orta dikmelerin kesişim noktası, üçgenin ağırlık merkezi ile örtüşür ki bu da bir üçgenin dengesi açısından önemli bir noktadır. Bu tür sorularla karşılaştığımda, kenar orta dikmenin özelliklerini kullanarak daha hızlı ve etkili çözümler bulabiliyorum.
Birdal,
Yorumunuzda kenar orta dikmenin tanımını ve özelliklerini oldukça iyi özetlemişsiniz. Bu konuda daha fazla bilgi vermek gerekirse, kenar orta dikmenin sadece üçgenlerde değil, aynı zamanda diğer çokgenlerde de önemli bir yer tuttuğunu belirtmek isterim. Kenar orta dikme, üçgenin simetrik özelliklerini anlamak için gerçekten faydalıdır, çünkü üçgenin simetrisi, birçok geometri probleminin temelini oluşturur.
Ayrıca, kenar orta dikmelerin kesişim noktasının ağırlık merkezi ile örtüşmesi, geometri derslerinde sıkça kullanılan bir özellik. Bu durum, üçgenin dengesi açısından kritik bir öneme sahiptir. Geometrik problemlerde bu tür özellikleri bilmek, daha karmaşık sorunların üstesinden gelmekte büyük avantaj sağlar.
Sonuç olarak, kenar orta dikmelerin özelliklerine dair derinlemesine bir anlayış geliştirmek, geometri bilgi seviyenizi artıracak ve problem çözme becerilerinizi güçlendirecektir. Başarılar dilerim!
Üçgenin yardımcı elemanları hakkında yazdıklarınızı okudum ve gerçekten de bu elemanların önemini deneyimleyerek anladım. Özellikle soruları çözerken kenarortay ve yükseklik gibi yardımcı elemanları kullanmanın ne kadar işe yaradığını fark ettim. Bu elemanlar sayesinde, bazı soruların daha hızlı ve pratik bir şekilde çözüldüğünü görmek beni çok mutlu etti. Özellikle dik üçgenlerdeki muhteşem üçlü özelliği, soruları çözerken en sık karşılaştığım durumlar arasında. Bu yardımcı elemanları kullanarak soruları çözmek, matematikteki karmaşayı azaltıp, daha net bir şekilde ilerlememi sağlıyor. Diğer yandan, açıortayların kullanımıyla açıları eşit parçalara bölerken, kenar orta dikme ile kenarları daha rahat analiz edebiliyorum. Bu durum, üçgenlerle ilgili çalışmalarda bana büyük avantaj sağladı. Sizin de belirttiğiniz gibi, bu yardımcı elemanların doğru kullanımı, geometri konusundaki başarımı artırıyor.
Merhaba Aligüher,
Yorumunuz için teşekkür ederim. Üçgenin yardımcı elemanlarının ne kadar önemli olduğuna dair deneyimlerinizi duymak çok güzel. Kenarortay ve yükseklik gibi elemanların soruları daha pratik bir şekilde çözmenize yardımcı olması gerçekten etkileyici. Özellikle dik üçgenlerdeki üçlü özelliğin sağladığı avantaj, matematiksel problemlerdeki karmaşayı azaltmak için harika bir yol.
Yardımcı Elemanların Kullanımı
Açıortayların kullanımıyla açıları eşit parçalara bölmek, gerçekten de analiz sürecini kolaylaştırıyor. Bu gibi stratejilerle, üçgenlerle ilgili çalışmalarınızda daha da başarılı olacağınızı düşünüyorum. Geometri konusundaki başarıyı artıracak bu tür pratik yaklaşımlar, matematiğin keyfini çıkarmanıza olanak tanıyor.
Bu konudaki görüşlerinizi paylaşmaya devam edin, deneyimlerinizi duymak her zaman keyifli. Başarılar dilerim!
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?