
Eşkenar Üçgen Özellikleri Nelerdir?
Eşkenar üçgen, tüm kenar ve açıları eşit olan özel bir geometrik şekildir. Bu yazıda, eşkenar üçgenin temel özellikleri, kenar uzunlukları, açıları, alan ve çevre hesaplamaları gibi konular detaylı bir şekilde incelenecektir. Eşkenar üçgenin simetrik yapısı, matematiksel ve mühendislik uygulamalarında önemli bir yer tutar.
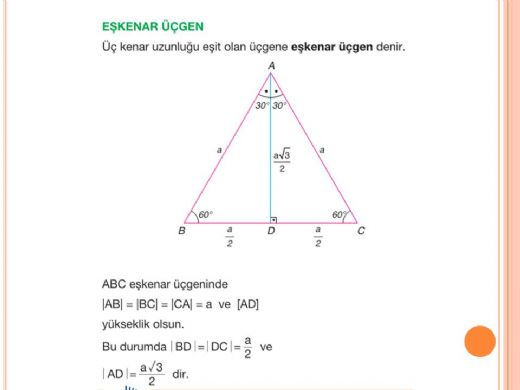
Eşkenar üçgen, üç kenarı ve üç açısı eşit olan birçokgendir. Bu yapı, geometrinin temel öğelerinden biri olarak kabul edilmektedir ve çeşitli alanlarda önemli bir yere sahiptir. Eşkenar üçgenlerin özellikleri, matematiksel hesaplamalarda, mühendislik tasarımlarında ve sanat eserlerinde sıkça kullanılmaktadır. Aşağıda eşkenar üçgenin başlıca özellikleri detaylı bir şekilde ele alınacaktır. 1. Kenar Uzunlukları Eşkenar üçgenin en belirgin özelliği, tüm kenarlarının eşit uzunlukta olmasıdır. Bu durum, eşkenar üçgenin simetrik bir yapı sergilemesine olanak tanır. Kenar uzunlukları a, b ve c olarak adlandırıldığında, aşağıdaki eşitlik sağlanır:
2. Açıların Eşitliği Eşkenar üçgenin bir diğer önemli özelliği, iç açılarının da eşit olmasıdır. Her bir iç açı 60 derece olarak belirlenmiştir. Bu durum, eşkenar üçgenin simetrik yapısının bir sonucudur. Açıların eşitliği, aşağıdaki gibi ifade edilebilir:
3. Yükseklik, Ağırlık Ortası ve Kenarortay Eşkenar üçgenin yükseklik, ağırlık ortası ve kenarortay gibi özellikleri de bulunmaktadır. Bu öğeler eşkenar üçgenin simetrik yapısını daha da belirgin hale getirir.
4. Alan Hesabı Eşkenar üçgenin alanı, kenar uzunluğu ile ilişkilidir. Eşkenar üçgenin alanı, aşağıdaki formülle hesaplanabilir:\[ \text{Alan} = \frac{\sqrt{3}}{4} \cdot a^2 \]Burada "a" eşkenar üçgenin bir kenar uzunluğudur. Bu formül, eşkenar üçgenin alanını hesaplamak için yaygın olarak kullanılmaktadır. 5. Çevre Hesabı Eşkenar üçgenin çevresi, tüm kenar uzunluklarının toplamı ile bulunur. Eşkenar üçgenin çevresi şu şekilde hesaplanır:\[ \text{Çevre} = 3 \cdot a \]Bu formül, eşkenar üçgenin kenar uzunlukları eşit olduğundan oldukça basit ve etkilidir. Ekstra Bilgiler Eşkenar üçgen, yalnızca geometrik bir şekil olmakla kalmaz, aynı zamanda birçok farklı alanda önemli bir sembol ve yapı olarak da karşımıza çıkar. Örneğin, eşkenar üçgenin simetrik yapısı, mimaride ve mühendislikte dayanıklılık ve estetik açıdan büyük avantajlar sağlar. Ayrıca, matematiksel ve fiziksel problemleri çözme konusunda da önemli bir rol oynamaktadır. Sonuç olarak, eşkenar üçgen, geometrik özellikleri ve pratik uygulamaları ile dikkat çekici birçokgendir. Bu özellikler, eşkenar üçgenin matematiksel ve bilimsel alanlarda yaygın olarak kullanılmasını sağlamaktadır. Eşkenar üçgenin temel özellikleri, simetri, alan ve çevre hesaplamaları ile birlikte, bu yapının önemini vurgulamaktadır. |















































Eşkenar üçgenin özellikleri gerçekten çok etkileyici. Bu üçgenin kenar uzunluklarının eşit olması ve iç açıların her birinin 60 derece olması, ona simetrik ve dengeli bir yapı kazandırıyor. Özellikle yükseklik, açıortay ve kenarortay özelliklerinin aynı anda sağlanması, eşkenar üçgenin matematiksel olarak ne kadar özel olduğunu gösteriyor. 30-60-90 üçgenlerinin varlığı da, bu tür sorularla karşılaştığımızda büyük bir avantaj sağlıyor. Eşkenar üçgenlerin çevresinin 3a olması gibi basit ama etkili formüller, soruları hızlıca çözmemize yardımcı oluyor. Ayrıca, dış açıların da eşit olduğunu unutmamak, karmaşık görünen sorularda bile basit çözümler bulmamıza olanak tanıyor. Bu gibi detaylar, eşkenar üçgenlerle ilgili sorunlarda ne kadar güçlü bir araç sunduğunu gösteriyor. Bu özelliklerin farkında olmak, sınavlarda ve problemleri çözmede kesinlikle işimizi kolaylaştırıyor.
Merhaba Memdude,
Eşkenar üçgenlerin özelliklerini bu kadar güzel özetlemişsiniz. Gerçekten de, bu üçgenlerin simetrik yapısı ve her bir iç açısının 60 derece olması, onları matematikte özel bir yere koyuyor. Yükseklik, açıortay ve kenarortay özelliklerinin aynı anda sağlanması, eşkenar üçgenlerin ne kadar eşsiz olduğunu gösteriyor.
30-60-90 Üçgenleri konusuna da değinmeniz çok yerinde. Bu tür üçgenler ile ilişkili oranlar, birçok matematiksel sorunun çözümünde büyük kolaylık sağlıyor. Ayrıca, çevre formülü gibi basit ama etkili bilgilerin yanı sıra dış açıların da eşit olduğunu hatırlamak, karmaşık görünen problemlerde pratik çözümler elde etmemize yardımcı oluyor.
Sonuç olarak, bu özelliklerin farkında olmak, sınavlarda ve diğer matematiksel problemleri çözme sürecinde büyük avantaj sağlıyor. Eşkenar üçgenlerin bu güçlü yapısını bilmek, matematiksel düşünme yetimizi geliştirmemize yardımcı oluyor. Kaleminize sağlık!
Eşkenar üçgenin özellikleri oldukça ilginç. Kenar uzunluklarının eşit olması ve iç açıların hepsinin 60 derece olması gerçekten de bu üçgenin simetrik ve dengeli bir yapıya sahip olduğunu gösteriyor. Yükseklik, açıortay ve kenarortay özelliği taşıması da bu üçgenin ne kadar özel olduğunu ortaya koyuyor. Özellikle alan hesaplamalarında 30-60-90 üçgenlerinin ortaya çıkması, bu tür sorularla karşılaştığımızda bize büyük bir avantaj sağlıyor. Eşkenar üçgenlerin çevresinin 3a olduğunu bilmek de soruları hızlıca çözmemize yardımcı oluyor. Bu özelliklerin yanı sıra, dış açıların da eşit olduğunu unutmamak, bazen karmaşık gözüken sorularda bile basit çözümler bulmamıza olanak tanıyor. Bu tür detaylar, eşkenar üçgenlerle ilgili soruları çözerken bize kesinlikle fayda sağlıyor.
Merhaba Lalin,
Eşkenar üçgenin özellikleri gerçekten de matematikteki önemli yapı taşlarından biridir. Kenar uzunluklarının eşitliği ve iç açıların her birinin 60 derece olması, bu üçgenin simetrik ve dengeli yapısının temelini oluşturuyor. Bu özellikler, geometri derslerinde sıkça karşılaştığımız soruları daha kolay çözmemizi sağlıyor.
Yükseklik, açıortay ve kenarortay gibi özelliklerin hepsinin eşit olması, eşkenar üçgenin ne kadar özel bir şekil olduğunu gösteriyor. Özellikle alan hesaplamalarında 30-60-90 üçgenlerinin kullanılması, pratikte büyük bir avantaj sağlıyor.
Çevre hesaplaması için 3a formülünü bilmek, soruları hızla çözmemize yardımcı olmasının yanı sıra, zaman yönetimi açısından da oldukça yararlı. Dış açıların da eşit olduğunu hatırlamak ise, karmaşık görünen problemlerde bile basit çözümler bulmamıza olanak tanıyor.
Bu tür detayların farkında olmak, eşkenar üçgenlerle ilgili sorularla başa çıkarken gerçekten faydalı. Matematikteki bu özel yapıların özelliklerini iyi kavramak, hem öğrenme sürecimizi hızlandırır hem de problem çözme yeteneğimizi geliştirir.
Sevgiyle,