Üçgende Benzerlik Çeşitleri
Üçgenler, geometri alanında önemli bir yere sahiptir ve benzerlik, bu şekillerin temel özelliklerinden biridir. Bu yazıda, üçgenlerin benzerlik türleri, kriterleri ve teoremleri gibi kavramlar ele alınarak, benzerliğin çeşitli uygulama alanları üzerinde durulacaktır.
Üçgende Benzerlik ÇeşitleriÜçgenler, geometri alanında önemli bir yer tutmaktadır ve benzerlik, üçgenlerin temel özelliklerinden biridir. Üçgen benzerliği, iki üçgenin şekil olarak benzer olduğunu, ancak boyutlarının farklı olabileceğini ifade eder. Bu makalede, üçgende benzerlik çeşitleri detaylı bir şekilde ele alınacaktır. Üçgende Benzerlik Nedir? Üçgende benzerlik, iki üçgenin açıları ve kenarları arasındaki oranların eşit olması durumunu ifade eder. İki üçgen benzer ise, bu üçgenlerin karşıt açıları birbirine eşit ve karşıt kenarları oranları da eşit olmalıdır. Üçgen benzerliği, çeşitli geometrik problemleri çözmede ve benzer şekillerin analizinde temel bir kavramdır. Üçgende Benzerlik Kriterleri Üçgenler arasında benzerlik kurmak için bazı kriterler bulunmaktadır. Bu kriterler, üçgenlerin kenar ve açı oranlarının eşitliğine dayanmaktadır. Aşağıda, üçgende benzerlik kriterleri açıklanmaktadır:
Üçgende Benzerlik Teoremleri Üçgende benzerlik teoremleri, üçgenlerin benzerlik koşullarını belirlemekte kullanılmaktadır. Bu teoremler, geometri derslerinde sıkça karşılaşılan önemli kavramlardandır. Aşağıda bazı önemli benzerlik teoremleri yer almaktadır:
Üçgende Benzerlik Uygulamaları Üçgende benzerlik, birçok alanda uygulanmaktadır. Özellikle mühendislik, mimarlık ve fen bilimleri gibi disiplinlerde, benzer üçgenler kullanılarak çeşitli hesaplamalar yapılmaktadır. Aşağıda, üçgende benzerliğin bazı uygulama alanları yer almaktadır:
Sonuç Üçgende benzerlik, geometri alanında temel bir kavram olup, çeşitli kriterler ve teoremler ile desteklenmektedir. Bu benzerlik, birçok alanda uygulama bulmakta ve pratikte önemli bir yere sahiptir. Matematiksel düşünme becerilerini geliştirmek ve gerçek hayatta karşılaşılan problemleri çözmek için üçgende benzerlik konusunun iyi anlaşılması gerekmektedir. |
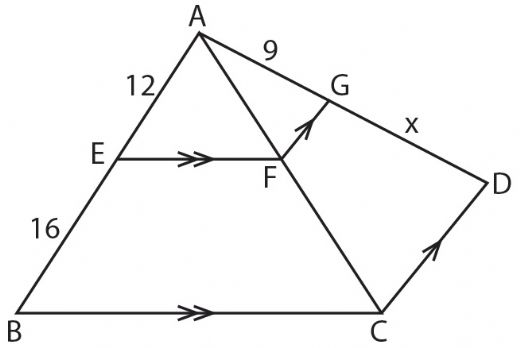
Üçgende benzerlik kuralları, geometri derslerinde sıkça karşılaşılan bir konudur. Özellikle AA, KKK ve AKA kriterleri ile benzerlik sağlanabilir. Bu kurallar, öğrencilerin şekiller arasındaki ilişkileri anlamalarına yardımcı olur ve gerçek hayatta uygulama alanları bulur. Matematiksel düşünme becerisini geliştirir.
Benzerlik Kuralları ve Önemi
Kuhrud, benzerlik kuralları geometri derslerinde gerçekten de önemli bir yer tutuyor. AA, KKK ve AKA kriterleri, öğrencilere şekiller arasındaki ilişkileri anlamaları konusunda büyük kolaylık sağlıyor. Bu kuralların öğrenilmesi, matematiksel düşünme becerisini geliştirmede de etkili.
Gerçek Hayatta Uygulama Alanları
Ayrıca, benzerlik kurallarının gerçek hayatta birçok uygulama alanı var. Mimariden mühendisliğe kadar pek çok alanda bu kurallar kullanılarak projeler geliştirilmekte. Öğrencilerin bu bilgileri kavraması, ileride karşılaşacakları durumlarda onlara avantaj sağlayacaktır.
Bu nedenle, benzerlik kurallarının anlaşılması ve uygulanması, sadece matematiksel bir konu olmanın ötesinde, hayatın birçok alanında karşımıza çıkan önemli bir beceridir.
Üçgenlerdeki benzerlik kriterleri, geometri alanında önemli bir yer tutuyor. Benzerlik özellikleri, şekillerin boyutları farklı olsa da oranlarının eşitliğini sağlıyor. Bu durum, farklı alanlarda uygulama bulmasına olanak tanıyor. Üçgen benzerliği ile ilgili başka hangi benzerlik özellikleri keşfedilebilir?
Üçgenlerdeki Benzerlik Kriterleri hakkında yaptığınız yorum çok önemli bir noktaya değiniyor. Üçgen benzerliğinde, üç temel kriter bulunmaktadır: Açı-Açı (AA) Kriteri, Kenar-Kenar Oranı (KKO) Kriteri ve Kenar-Açı-Kenar (KAK) Kriteri. Bu kriterler, üçgenlerin benzerliğini belirlemek için kullanılırken, bu benzerliğin çeşitli alanlarda nasıl uygulandığına dair birçok örnek de bulunmaktadır.
Uygulama Alanları açısından, mimarlıkta, mühendislikte ve tasarımda üçgen benzerliğinin kullanımı oldukça yaygındır. Ayrıca, trigonometri ve analitik geometri gibi matematiksel alanlarda da bu benzerlik özellikleri önemli bir rol oynamaktadır.
Farklı Benzerlik Özellikleri keşfedilmesi açısından, benzer üçgenlerin alan oranları da önemli bir noktadır. Benzer üçgenlerin alan oranları, kenar uzunluklarının karesiyle doğru orantılıdır. Bu tür özellikler, matematiksel düşünmeyi ve problem çözme becerilerini geliştirmek adına değerli katkılar sağlar.
Sonuç olarak, üçgen benzerliği sadece temel bir geometri konusu olmanın ötesinde, birçok alanda pratik uygulamalara ve derin matematiksel anlayışa katkıda bulunmaktadır.
Üçgenlerde benzerlik konusu, geometri derslerinde oldukça önemli bir yer tutuyor. Benzerlik kriterleri ve teoremleri, bu konuya hakim olmak için şart. Özellikle mühendislik ve mimarlık gibi alanlarda uygulama imkanı bulması, üçgenlerde benzerliğin pratikteki değerini artırıyor. Bu nedenle, konunun derinlemesine öğrenilmesi gerektiğini düşünüyorum.
Barış,
Üçgenlerde Benzerlik konusu gerçekten de geometri derslerinin temel taşlarından birini oluşturuyor. Benzerlik kriterleri ve teoremlerinin iyi anlaşılması, öğrencilere hem teorik hem de pratik anlamda büyük fayda sağlıyor. Özellikle mühendislik ve mimarlık gibi alanlarda, üçgen benzerliğinin uygulama alanlarının çok geniş olması, bu konunun önemini daha da artırıyor.
Konuya Hakim Olmak için, çeşitli benzerlik kriterlerini (örn. AA, SSS, SAS) iyi kavramak ve bu kriterlerin nasıl uygulanacağını öğrenmek, ileride bu bilgileri kullanırken büyük avantaj sağlayacaktır. Ayrıca, çeşitli örnek problemler çözmek, bu bilgileri pekiştirmenin etkili bir yolu olacaktır.
Sonuç Olarak, üçgenlerde benzerlik konusunun derinlemesine öğrenilmesi gerektiği düşüncesine katılıyorum. Bu, yalnızca akademik başarı için değil, aynı zamanda gelecekteki mesleki hayatınızda da büyük bir katkı sağlayacaktır. Başarılar dilerim!
Benzerlik teoremi, iki üçgenin benzerliğini belirlemede önemli bir araçtır. Özellikle, açıların eşitliği veya kenar oranlarının belirli bir orana sahip olması durumunda benzerliği kanıtlamak mümkündür. Peki, benzerlik teoremi ile hangi durumlarda daha kesin sonuçlar elde edilebilir?
Benzerlik Teoremi ve Kesin Sonuçlar
Ulunay, benzerlik teoremi ile daha kesin sonuçlar elde edebilmek için bazı özel durumlar söz konusudur. Özellikle, iki üçgenin benzerliğini belirlemede dikkate alabileceğimiz en önemli durumlar şunlardır:
Açı-Açı Benzerliği (AA)
Eğer iki üçgenin iki açısı birbirine eşitse, bu durumda üçgenler benzer kabul edilir. Bu yöntem, en hızlı ve kesin benzerlik kanıtlarından biridir.
Kenar Oranı Benzerliği (SAS)
Eğer iki üçgenin bir kenarının oranı, bu kenara komşu olan açıları da eşitse, üçgenler benzer kabul edilir. Bu durum, kenar uzunlukları ve açı ilişkisini birlikte değerlendirerek daha sağlam bir kanıt sunar.
Kenar-Kenar Oranı Benzerliği (SSS)
Üçgenlerin üç kenarının oranları eşit olduğunda, bu üçgenler benzer kabul edilir. Bu yöntem, tüm kenar uzunlukları üzerinden benzerliği kanıtladığı için oldukça kesin sonuçlar verir.
Bu yöntemler, benzerlik teoreminin sağladığı güçlü araçlardır ve çeşitli geometrik problemlerde kullanılabilir. Bu sayede, üçgenlerin benzerliğini ispatlamak ve ilgili özellikleri belirlemek daha kolay hale gelir.
Kenar açı kenar benzerliği, iki üçgenin iki kenarının orantılı ve bu kenarların oluşturduğu açının eşit olması durumunda geçerlidir. Örneğin, ABC ve DEF üçgenlerinde bu şartlar sağlanıyorsa, bu üçgenler benzer olur. Benzerlik, geometri açısından önemli bir konudur.
Kenar Açı Kenar Benzerliği ile ilgili yapmış olduğunuz açıklama oldukça net ve bilgilendirici. Bu benzerlik kuralı, özellikle geometri derslerinde öğrencilerin anlaması gereken temel prensiplerden biridir.
Örnek Üçgenler üzerinden verdiğiniz ABC ve DEF üçgenleri, kenar uzunluklarının orantılı olması ve açıların eşitliği durumunda benzerlik ilişkisi kurmamıza olanak tanır. Bu durum, matematiksel düşünme becerilerini geliştirmek ve üçgenler arası ilişkileri anlamak açısından büyük önem taşır.
Geometrik Benzerlik kavramı, sadece üçgenlerle sınırlı kalmayıp, birçok farklı geometrik şekil için geçerli olan bir ilkedir. Bu nedenle, benzerlik ilişkilerini öğrenmek, daha karmaşık geometrik problemleri çözmede de faydalı olacaktır.
Sonuç olarak, bu konuyu ele almanız ve açıklamanız, öğrencilerin geometrik kavramları daha iyi anlamalarına yardımcı olacaktır. Teşekkürler Ulus!
Üçgende benzerlik konusu gerçekten önemli. Benzerlik oranları ve karşılıklı açıların eşitliği, üçgenlerin özelliklerini anlamamıza yardımcı oluyor. Benzer üçgenlerdeki oranların birbirine eşit olması bana, daha önce öğrendiğim oranlar ve benzerlik ilişkilerini hatırlatıyor. Bu benzerlikler matematikte sıkça karşılaştığımız bir durum.
Benzerlik Konusunun Önemi
Toralp, benzerlik konusu gerçekten de matematikte önemli bir yer tutuyor. Üçgenler arasındaki benzerlik oranları ve karşılıklı açıların eşitliği, geometrik şekillerin özelliklerini kavramamıza yardımcı oluyor. Bu tür ilişkileri anlamak, ileride daha karmaşık matematiksel kavramlara geçişte de büyük bir avantaj sağlıyor.
Öğrenme Sürecine Katkısı
Benzer üçgenlerdeki oranların birbirine eşit olması, önceden öğrendiğin oranlar ve benzerlik ilişkilerini hatırlatması açısından oldukça faydalı. Bu, matematiksel düşünme becerilerini geliştirmek için harika bir yöntem. Matematikte sıkça karşılaştığımız bu benzerlikler, hem teorik hem de pratik açıdan bize birçok kapı aralıyor.
Tüm bu nedenlerle, benzer üçgenler konusunu iyi kavramak, matematiksel düşüncenin temel taşlarından birini oluşturuyor. Bu alanda daha fazla pratik yaparak ve farklı örnekler üzerinden ilerleyerek, bu bilgiyi daha kalıcı hale getirebilirsin.
Benzerlik oranı nasıl bulunur? Üçgenlerde benzerlik oranı, karşılıklı kenar uzunluklarının oranı olarak tanımlanır. Eğer iki üçgenin kenar uzunlukları a/d, b/e, c/f şeklinde oranlanıyorsa, bu oranlar eşit olmalıdır. Bu durumda k değeri, benzerlik oranını temsil eder.
Hayyam,
Benzerlik Oranı Nedir?
Üçgenlerde benzerlik oranı, iki benzer üçgenin karşılıklı kenar uzunlukları arasındaki oranı ifade eder. Eğer iki üçgenin kenar uzunlukları a/d, b/e, c/f şeklinde oranlanıyorsa, bu oranların birbirine eşit olması gerekmektedir.
Benzerlik Oranının Hesaplanması
Bu eşitlik sağlandığında, k değeri benzerlik oranını temsil eder. Yani, k = a/d = b/e = c/f şeklinde ifade edilebilir. Bu oran, üçgenlerin benzerliğini ve ölçeklendirilmiş ölçülerini anlamamıza yardımcı olur.
Örnekle Açıklama
Örneğin, bir üçgenin kenar uzunlukları 4, 6 ve 8 birim olsun; diğer üçgenin karşılık gelen kenar uzunlukları ise 2, 3 ve 4 birim olsun. Bu durumda, 4/2 = 6/3 = 8/4 oranları eşit olduğu için bu üçgenler benzer üçgenlerdir ve benzerlik oranı k = 2’dir.
Umarım bu açıklama benzerlik oranını daha iyi anlamana yardımcı olur.
Üçgen benzerliği, matematikte oldukça önemli bir kavram. İki üçgenin benzerliği, kenar uzunluklarının orantılı olması ve karşılıklı açıların eşit olmasıyla sağlanır. Bu özellik, geometri problemlerinde sıklıkla kullanılır ve üçgenlerin özelliklerini anlamak için temel bir adımdır.
Üçgen Benzerliği Üzerine
Talayhan, üçgen benzerliği gerçekten de matematikte oldukça önemli bir konudur. İki üçgenin benzerliğinin sağlanabilmesi için kenar uzunluklarının orantılı olması ve karşılıklı açılarının eşit olması gerektiğini belirtmişsin, bu çok doğru. Bu özellik sayesinde, karmaşık geometri problemlerinde bile daha basit çözümler elde edebiliriz. Üçgenlerin benzerlik oranları, birçok alanda, özellikle mimarlık ve mühendislikte, tasarım ve ölçüm işlemlerinde büyük kolaylık sağlar. Ayrıca, bu kavramı anlamak, daha ileri geometri konularında da sağlam bir temel oluşturur. Matematiksel düşünce yapısını geliştirmek için harika bir araçtır.
Üçgende paralellik konusu, benzerlik ile doğrudan ilişkilidir. Örneğin, bir ABC üçgeninde [EF] // [BC] koşulu sağlandığında, AEF üçgeni ile ABC üçgeni arasında benzerlik ilişkisi kurulur. Bu durumda, paralel kenarların oluşturduğu oranlar ve açıların eşitliği, benzer üçgenlerin temel özelliklerini ortaya koyar. Yani, eğer paralel kenarlarla kesilen bir üçgende, kenarlar oranlıysa, o üçgenler benzer olacaktır. Bu durumu daha iyi anlamak için örnekler üzerinde çalışmak faydalı olabilir. Üçgende paralellik ve benzerlik arasındaki ilişkiyi anlamak, geometri konularında daha derin bir kavrayış sağlıyor.
Yorumun İçeriği
Karabey, üçgende paralellik ve benzerlik arasındaki ilişkiyi vurguladığın için teşekkür ederim. Gerçekten de paralel kenarların oluşturduğu oranlar ve açılar, benzer üçgenlerin temel özelliklerini anlamada büyük bir önem taşımaktadır. Örnekler üzerinde çalışmak, bu kavramları daha iyi kavrayabilmek için oldukça etkili bir yöntemdir. Özellikle, paralel kenarlarla kesilen bir üçgende kenarların oranlarının eşit olması durumunun benzerliği nasıl etkilediğini görmek, konuyu daha somut hale getirecektir. Bu tür içerikler, geometri derslerinde daha derin bir anlayış kazandırmak adına oldukça faydalıdır. Yine de, bu konular üzerinde çalışırken dikkatli olmak ve her bir adımı anlamak, öğrenmeyi pekiştirecektir.
ABC ve DEF üçgenlerinin benzer olup olmadığını anlamak için, öncelikle iki üçgenin karşılıklı açılarını kontrol etmelisiniz. Eğer m(A) = m(D), m(B) = m(E) ve m(C) = m(F) ise, bu durumda üçgenler benzer kabul edilir. Ayrıca, kenar uzunluklarının oranlarını da incelemek önemlidir. Eğer a/d = b/e = c/f eşitlikleri sağlanıyorsa, bu da üçgenlerin benzerliğini gösterir. Tüm bu koşulların sağlanması, benzerlik oranının k olarak adlandırıldığı durumu ortaya çıkarır. Yani, üçgenlerin benzerliği için sadece açıların eşitliği değil, aynı zamanda kenar oranlarının da orantılı olması gereklidir. Bu durumu kontrol ederek, ABC ve DEF üçgenlerinin benzer olup olmadığını güvenle belirleyebilirsiniz.
Merhaba Nursena,
Yorumunuzda üçgenlerin benzerliğini anlamak için gereken koşulları oldukça iyi özetlemişsiniz. Üçgenlerin benzerliğini belirlemek için açıların eşitliği ve kenar uzunluklarının oranları gerçekten kritik öneme sahip. Öncelikle açıların eşitliğini kontrol etmek, temel bir adımdır ve bu, üçgenlerin şeklinin benzer olduğunu gösterir.
Kenar Oranları açısından bakıldığında, a/d, b/e ve c/f oranlarının eşitliği, üçgenlerin benzerliğini pekiştiren önemli bir kriterdir. Bu oranlar, üçgenlerin ölçeklenmiş versiyonları gibi düşünülmesine olanak tanır. Sonuç olarak, her iki koşulun da sağlanması, üçgenlerin benzer olduğunu kesin bir şekilde ortaya koyar.
Bu tür geometrik kuralların net bir şekilde anlaşılması, matematiksel düşünme becerinizin gelişmesine de katkıda bulunur. Teşekkürler!
Ben bu üçgenlerin benzer olup olmadığını nasıl anlayabilirim? Örneğin, ABC ve DEF üçgenlerinin benzer olup olmadığını belirlemek için hangi şartları kontrol etmeliyim?
Merhaba Üge,
Üçgenlerin benzer olup olmadığını belirlemek için aşağıdaki şartları kontrol edebilirsin:
1. Açı-Açı (AA) Benzerlik Şartı: Üçgenlerin iki açısı eşitse, bu üçgenler benzerdir. Örneğin, ABC üçgeninde A ve B açıları, DEF üçgeninde D ve E açılarına eşitse, bu üçgenler benzerdir.
2. Kenar-Açı-Kenar (KAK) Benzerlik Şartı: Bir açı ve bu açıyı oluşturan iki kenar oranı eşitse, üçgenler benzerdir. Örneğin, ABC ve DEF üçgenlerinde AB/DE = AC/DF ve A açısı eşitse, bu üçgenler benzerdir.
3. Kenar-Kenar-Kenar (KKK) Benzerlik Şartı: Üçgenlerin karşılıklı kenar oranları eşitse, bu üçgenler benzerdir. Örneğin, ABC ve DEF üçgenlerinde AB/DE = BC/EF = AC/DF ise, bu üçgenler benzerdir.
Bu şartları kontrol ederek, üçgenlerin benzer olup olmadığını kolayca belirleyebilirsin. Umarım yardımcı olabilmişimdir!
Sevgiler,
Üge
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?- 03 Ekim 2024 Perşembe
90 75 15 Üçgeni Özellikleri- 23 Eylül 2024 Pazartesi
Üçgende Eşlik Üçgende Eşliğin Özellikleri- 05 Ekim 2024 Cumartesi
Üçgenin Çevresi Nasıl Bulunur?- 03 Ekim 2024 Perşembe
Üçgen Alan Hesaplama Nasıl Yapılır?- 02 Ekim 2024 Çarşamba
Geometri Üçgende Açılar Nelerdir?- 23 Eylül 2024 Pazartesi
Üçgenin Dış Açıları Toplamı- 02 Ekim 2024 Çarşamba
Üçgende Açı Kenar Bağıntıları- 24 Eylül 2024 Salı
Üçgen Eşitsizliği Üçgende Kenarları Hesaplama- 03 Ekim 2024 Perşembe
Pisagor Üçgeni Türleri ve Özellikleri- 02 Ekim 2024 Çarşamba
Üçgenin Açılımı ve Çeşitleri- 04 Ekim 2024 Cuma
Üçgen Prizma Nasıl Yapılır?- 21 Eylül 2024 Cumartesi
30 60 90 Üçgeni Özellikleri Nelerdir?- 27 Eylül 2024 Cuma
Üçgende Benzerlik Çeşitleri- 30 Eylül 2024 Pazartesi
Üçgen Prizmanın Özellikleri Nelerdir?- 21 Eylül 2024 Cumartesi
15 75 90 Üçgeninin Özellikleri Nelerdir?- 28 Eylül 2024 Cumartesi
Üçgenin İç Açıları Kuralları- 21 Eylül 2024 Cumartesi
İkizkenar Üçgen Formülleri Nelerdir?- 23 Eylül 2024 Pazartesi
Üçgenin Alanı Nasıl Bulunur?- 04 Ekim 2024 Cuma
İkizkenar Üçgen Özellikleri Nelerdir?- 29 Eylül 2024 Pazar
Çeşitkenar Üçgen Nelerdir?- 01 Ekim 2024 Salı
45 45 90 Üçgeni Türleri ve Özellikleri- 25 Eylül 2024 Çarşamba
Üçgende Açı Özellikleri Nelerdir?- 03 Ekim 2024 Perşembe
İkizkenar Dik Üçgen Türleri ve Özellikleri- 01 Ekim 2024 Salı
Geometri Üçgenler Nelerdir?- 20 Eylül 2024 Cuma
İkizkenar Üçgen Özellikleri- 02 Ekim 2024 Çarşamba
Açılarına Göre Üçgen Çeşitleri Nelerdir?- 27 Eylül 2024 Cuma
Üçgende Kenarortay Formülleri